半年零基础到 LeetCode 300 题，我的算法学习方法论

今天终于又开了一个大坑，小染的零基础算法面试指南。作为一个去年刚转码的半路出家选手，摸爬滚打半年多零基础学 Java 到年底刷完了 300 LeetCode 算法题，总结了不少思路，也体验过算法学习入门过程的痛苦。因此想写一个对于零基础友好的算法面试学习指南，希望能分享自己的思考与经验，给准备算法面试的大家以帮助，欢迎一起交流讨论。

文章会按照自己整理的题目分类，使用 Java 语言，根据自己学习过程中总结的比较友好易于理解的顺序进行更新，带你从零开始培养算法思维和准备面试，争取解决一道题的同时解决一类题。由于我的 CS 知识都是在国外这边课程学习的，很多名词我也不是很清楚中文的准确翻译是什么，因此为了避免歧义有些地方会使用英文 term。最后题目可以分析清楚，code 可以 bug free，follow-up 能够接得住，那么就达到了目的。

我的 Github 中可以阅读文章中的代码及下载进行本地调试。如果有用的话，欢迎给我的 Repo 点个 Star。

作为算法系列文章的开篇，今天我们就来聊一聊算法与数据结构的学习思路，当我们在准备算法面试时到底在准备什么。

1. 究竟什么是算法

本科时由于天天在实验室做反应，对 CS 是一点兴趣没有，C++ 考试也是超低分飘过。一度觉得自己不可能再碰这些东西，没想到最后一语成谶。以前总觉得算法特别高大上，是普通人没法去接触开发的东西，实际入门之后才发现，算法其实无他，就只是解决问题的方法而已。

问：将大象放进冰箱需要几步？

收到任务 → 打开冰箱门 → 把大象放进去 → 关上冰箱门 → 报告任务完成

这就是一个算法。只要有一系列定义好的清晰步骤，并且可以在有限的时间及空间内执行完毕，那么它就是一个有效的算法。

算法是为了解决实际问题可提出，并经过推演证明，优化提高，再到具体实现。对于复杂的问题，算法也自然而然非常复杂，也因此我们会需要去学习一些以前的大牛们所研究出来的算法，站在巨人的肩膀上思考问题。

算法是描述 state 的转移和变化

这句话在一开始似乎显得有些废话，在学习了一段时间后，自己愈发加深了对 state 的理解。其实宏观上来看算法是解决问题的步骤，微观来看算法就是通过 states 间的转移变化来完成任务。算法永远是从 initial state 出发，经由一系列 well-defined successive states 最终完成既定任务停止在 final state。

如果将化学反应机理类比为算法，在化学反应中我们从反应物 initial state 出发，经由一些步骤产生不同的 intermidiates 中间态，最终完成所有步骤得到生成物 final state。

我们实际的算法运行过程也可以细化到每一个时间状态下的 state，即每一行代码的运行都会改变 state 从而执行我们所 well-defined 的步骤。

小到Linked List 和 Tree 操作过程中的 node 的改变，Two Pointers 在遍历数组或 String 时对元素的修改，大到 Dynamic Programming 中的状态转移方程，Backtracking 中每次尝试完一种选择后回溯到原来的 state ，都是藉由 state 的改变来执行完任务。只不过一个是局部的 state 改变，一个是整体的 state 改变。如果从这个角度来思考，算法似乎就没那么抽象了。

算法时间复杂度和空间复杂度

由于算法在有限的时间及空间内运行，因此我们需要来评价具体的算法优劣。具体的评价方式也是基于我们所有限的资源，即时间和空间，『运行快不快，空间省不省』。

时间复杂度

时间复杂度用于衡量算法『快不快』，是随着 input size 的规模变化而相对变化的一种趋势。面试中的时间复杂度我们一般使用 Big O 即​ $O(n)$ 来表示，Big O 并不表示代码真正的执行时间，而是一个相对的概念，表示运行时间随着 input 规模的变化的渐进趋势。

当规模 n 非常大时，$O(f(n))$ 中 $f(n)$ 里的低阶、常量、系数都不会左右增长趋势，增长渐进趋势决定于最大量级。

如 $O(n^2+3n+3)\rightarrow O(n^2)$ 。

一般情况下我们要分析的是 Worst Case Time Complexity，因为会反映了程序所能承受的上限。但实际上对于 QuickSort，Quick Partition 类的算法也要考虑 Average Case Time Complexity，因为这些算法虽然 Worst Case Time Complexity 很高，但是一般来说平均性能很优秀，因此也要考虑平均的情况。

空间复杂度

时间复杂度用于衡量算法『省不省』，一般我们讨论的是 Auxiliary space complexity，即算法额外使用的空间随着 input 的变化而相对变化的趋势。一般我们不会将 input 和 output 算在空间复杂度之内，但是如果需要额外的数据结构来存储算法过程当中的中间结果，一般来说是算入额外的空间复杂度中。和时间复杂度一样，空间复杂度也是一个相对概念。

算法是转专业最容易上手的部分

正如前面所说，算法就是解决问题的逻辑和实现，这个能力其实是相通的，无论是各行各业，我们都潜移默化练习培养着自己的 problem-sovling 的能力，只不过之前所研究的都是自己 domain 的问题。而现在我们所处理的算法问题，更多是一个 general 的需要解决的问题，因此我们的思路和能力也是可以转移过来的。而在转专业找工作过程中，相比其他需要积累的专业知识，个人觉得算法是最容易上手和学习的。

根据自身的思考习惯，是自上而下，还是自下而上，我们有两种将问题 boil down 为小问题的思路。是优先细节分析，还是长于整体考虑，我们也有 Iterative 和 Recursion 两种思考方式。具体如何细化操作，需要我们一些数据结构知识的辅助，但是这些都只是 Implementation 层面的问题，具体的算法是 Semantic 层面的思考，也因此我们也会看到有伪代码的存在，只是一个 code 化的步骤梗概。

Semantic and implementation

我认为在一开始学习算法和数据结构时，就将 Implementation 和 Semantic 分离开进行思考。不要觉得『Python/C++/Java 不好所以不会写这道题』，会不会做这道题和你会什么编程语言没有任何关系，不会做是因为你的逻辑层面就没有思考清楚怎么做，具体到实现层面就更不必说。Semantic 是我们的算法想要通过怎样的逻辑完成什么样的事，implementation 是具体到程序的实现层面，需要考虑 overhead 开销和执行效率等各种问题。

算法和数据结构是编程的基础也是基本功的体现，算法和数据结构二者组成了程序的实现本身。下面我来分享一下我学习过程中自己所思考整理的常见数据结构与算法总结，在 CS 知识的定义下不一定那么严谨，但是可以给我们初学者提供一个很好的概览和思路。

2. 数据结构的学习方法论

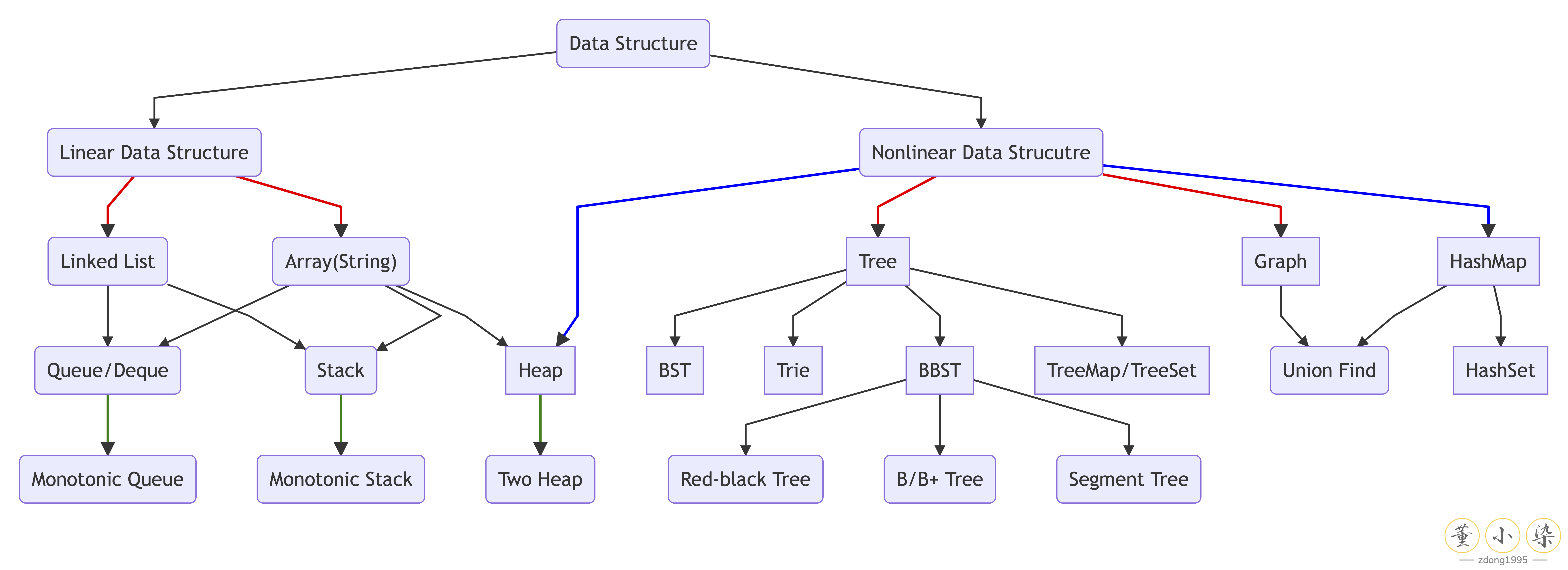
常用数据结构有 Array，LinkedList，Tree，Stack，Queue，Heap，Map，Set，Graph 及高级数据结构 Trie，Balanced BST，Union Find 等。但其实归根到底，自顶向下来看，数据结构就只有两种：线性数据结构和非线性数据结构。

一维线性数据结构

线性数据结构就是 LinkedList 和 Array 及其实现的一系列线性数据结构。任何数据结构归根到底都要么是通过 Array 来实现，要么是通过 LinkedList 来实现。

Array

Array 就是我们常见的数组，在计算机中在Array 在逻辑上和物理地址上都是连续的，可以类比为『一排箱子』，每个箱子里放了对应的元素。Array 不仅只能装数字，还可以装其他的各种 Object。

1

int[] arr = {10, 2, 26, 5};

String 也可以理解为 Array，因为 String 就是一个存 Character 字符的 Array，也因此大部分 String 的题目都可以将 String 转变为 Character Array 解决。

LinkedList

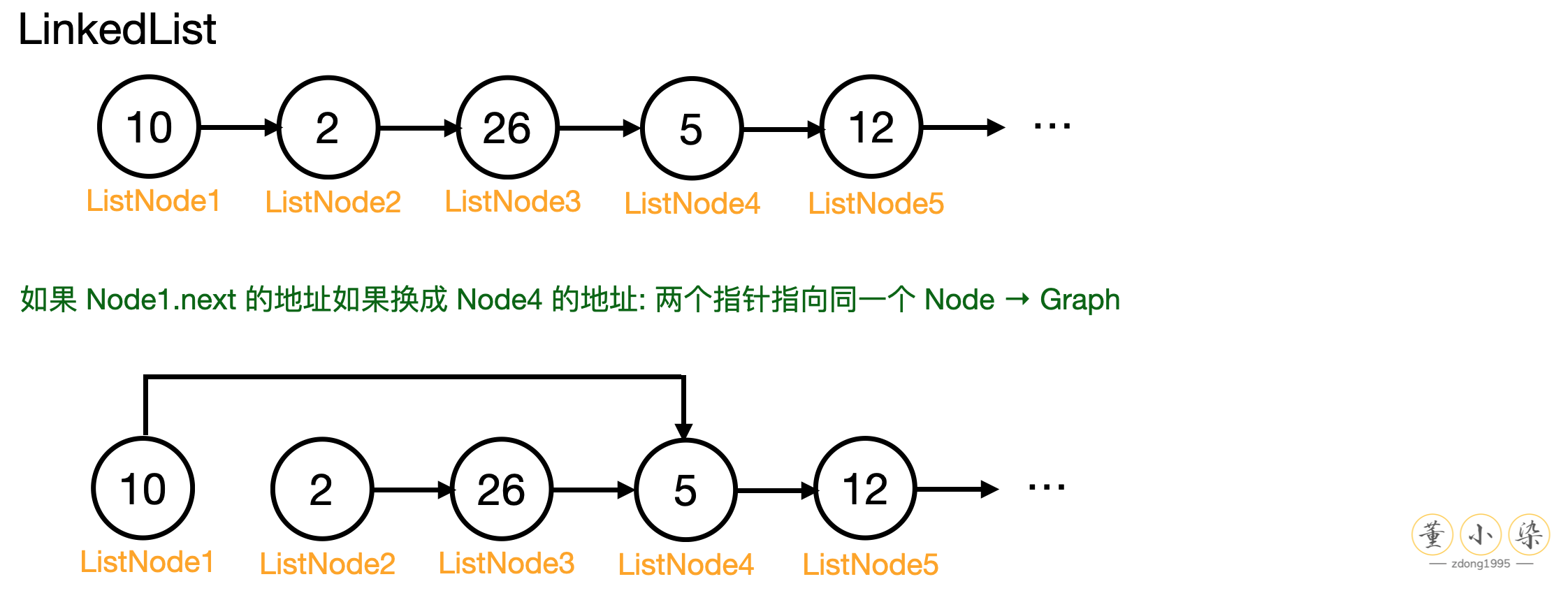
LinkedList 是在逻辑上连续的数组，但是在物理地址上并不是像 Array 一样连续的。LinkedList 包含一系列 ListNode：

1
2
3
4

class ListNode {
  int val;
  ListNode next;
}  

每一个 Node 有一个 next 的 field 存储下一个 Node 的引用地址，因此可以顺着当前 Node 找到下一个 Node。因此可以将 LinkedList 类比为『一堆箱子』，每个箱子里存放的是元素和下一个箱子的名片，也因此可以将 ListNode 穿成一串，实现 Array 一样的逻辑。

一般来说，我们的 LinkedList 都是 Singlely LinkedList，也就是单向的 1 v 1 关系。如果有多对一或一对多的关系，那么 LinkedList 就会变成图 Graph。如果图中没有环而且是全联通 fully connected，只有一个 source node，那么这种特殊的 Graph 就变成了我们一种重要的数据结构，Tree。这也就是从一维线性到非线性的过程，复杂的数据结构都是通过基础的一维线性数据结构组成。

有了 Array 和 LinkedList 这两个数据结构后，我们就可以实现并衍生出其他有需求的数据结构。这些具体的数据结构在后面我也会分享一下一步一步手写实现，来深入理解这些数据结构的底层结构。

• Queue：队列，是一种逻辑上的数据结构。维持先进先出 First In First Out (FIFO)，可以通过 Circular Array 或 LinkedList 进行实现。
• Deque：双端队列，两头都可以进出的队列。Java 的 Deque 实现也是有两种，ArrayDeque 和 LinkedList，其中 ArrayDeque 也是基于 Array 进行实现。
• Stack：栈，也是一种逻辑上的数据结构。维持先进后出 First In Last Out (FILO)，也可以通过 Array 或 LinkedList 进行实现。

整体来说，Array 实现由于内存连续分布，随机读写性能会更好，只需要 $ O(1)$时间即可完成。而 LinkedList 的实现需要额外的内存存储 next ，而且每次都需要从头往后找，因此会更消耗内存且读写性能会差一些。如果找最后的元素，worst case 会达到 $O(n)$ 的时间复杂度。

但是由于 Array 每次都是固定好 size 的内存空间，因此增删元素会显得麻烦一些，如果超过了 Array 的长度就需要处理扩容的问题。如果创建一个新的两倍容量的 Array，再将原来的 Array 中元素复制进去，就需要 $O(n)$ 的时间。 而 LinkedList 由于内存不连续没有后顾之忧，只需要创建一个新的箱子，将『新箱子的名片』发回给上一个箱子即可，可以进行 in-place 的操作，因此增删操作会更加 handy 一些，只需要 $O(1)$ 的时间即可。

非线性数据结构

上面提到了一维数据结构 LinkedList 将箱子里的『名片』从一张名片变成『多张名片』，那么就得到了非线性的数据结构 Tree 和 Graph。

Tree

对于常见的二叉树 Binary Tree，每一个 Node 最多有两个孩子，因此其中 TreeNode 包含的元素如下：

1
2
3
4
5

class TreeNode {
  int key;
  TreeNode leftChild;
  TreeNode rightChild;
}

因此每一个 TreeNode 存两张名片：『左孩子的名片和右孩子的名片』。

如果是多叉树 K-nary Tree 呢？将两个名片换成一个名片的 List 或者 Array 即可：

1
2
3
4
5

class TreeNode {
  int key;
  TreeNode[] children;
  // List<TreeNode> children
}

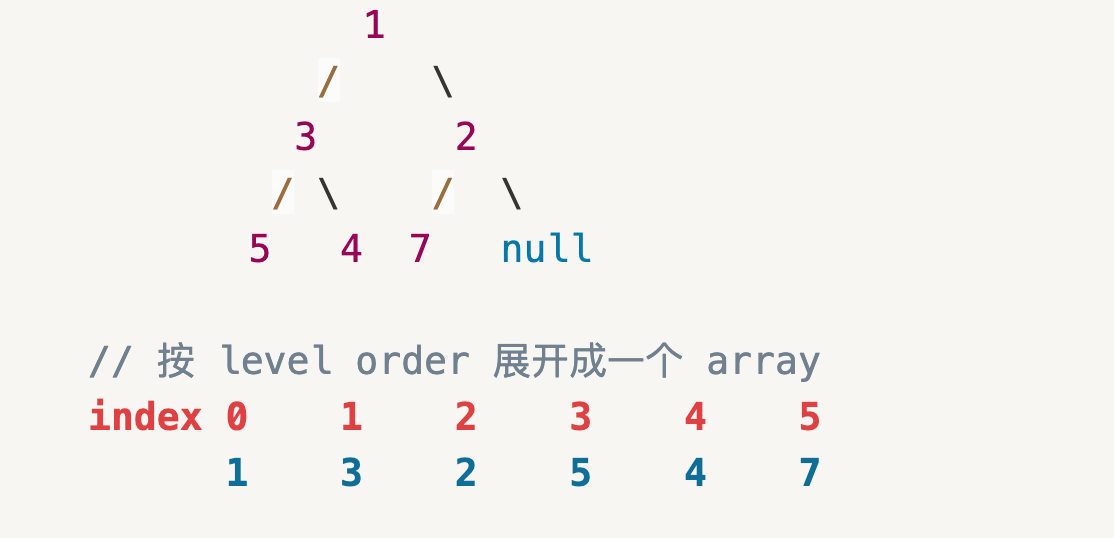
这里有一个特殊的数据结构，Heap。

Heap 在逻辑上是一颗树，物理存储为一个 unsorted array，是将 heap 按 level order (一层一层) 展开得到的一个线性排列。Semantic 来讲 Heap 是一个 Complete Binary Tree，即每层都是满的，唯一的空 Node 位置只会出现在最后一层的右侧 Leaf Node 上。

正是由于 Complete Binary Tree的性质，因而可以实现逻辑上和物理上的统一，能够保证 Heap 始终可以转换为一个 Level-order unsorted array，因此可以使用数学公式使用 $O(1)$ 的时间找到某一 Node 的左右 child 或找到左右 child 的 parent node。

• index of leftChild: $index_{leftChild} = index_{parent}\times 2 + 1$
• index of rightChild: $index_{rightChild} = index_{parent}\times 2 + 2$

Graph

同理，我们如果将 K-nary Tree 中的 children 变成 neighbors 就得到了 Graph:

1
2
3
4

class GraphNode {
  int val;
  List<GraphNode> neighbors;
}

如果你存了对方的名片，对方却不存你名片，那么就是单相思的『有向图』。如果所有人都互相存了名片，那么就是万物互联的『无向图』。

HashMap

最后就是一种非常非常重要的非线性数据结构，HashMap。可以说 Map 是数学家们所发明出来的最精巧的数据结构，也是面试中非常重要的数据结构。

HashMap 也叫 HashTable，用于存储 <key, value> 这样的 pair，会将一系列 key 通过 Hash Function 这样的一个映射函数将每一个 key 计算得到一个 unique 的 Hash 值，再经过一个 Hash Fucntion 将 Hash 值映射得到一个 index，将该 key 对应的 value 存储在 HashTable 内部的 Array 该 index 的位置。

但是实际上这个神奇的 Hash Function 并没有那么靠谱，Bukcet 是有限的，一定会有可能将不同的元素映射到同一个 index 中，也就是发生 collision 问题。为了处理这个问题，我们在 Array 中实际存储的不是单纯一个 value，而是一个 LinkedList 的 head 的引用地址。每次将一个 pair 映射到该 index，就将 value 添加到该位置的 LinkedList 中。

因此，HashMap 这样的巧妙结构可以通过数学计算，把数据的存储和查找所耗费的时间大大降低，在 $O(1)$ 的时间内可以找到某一个 key 所对应的 value。后面我们也会练习自己实现一个哈希表，来深入理解内部的原理。

同时衍生的另一种数据结构 HashSet，就和我们认识中的集合一样，不允许重复元素，因此可以用于查重操作。HashSet 的实现是 HashMap，区别是仅存储了 Key，没有存 Value。

至此我们可以看到，数据结构那么多种，Top-down 来看其实就是线性和非线性数据结构两大类。Bottom-up 来看，数据结构都是由 LinkedList 和 Array 这两种基础的数据结构实现。在实际使用过程中，还会有单调栈，单调队列，大小双堆等使用技巧，以及 Binary Search Tree，Balanced Binary Search Tree 和 Trie 这些高级 Tree 结构，后面遇到了再详细讲解。

在我们了解了常见的数据结构后，我们就需要学习如何利用这些数据结构来解决实际问题，因此就需要算法来运用合适的数据结构来处理问题，针对不同的数据类型也需要不同的算法。网站开发过程中有 CRUD 的说法，即 Create Read Update Delete，我们的算法实际上所做的也是通过对数据结构的增删改查来解决给定的问题。下面来总结一下常见算法及学习思路。

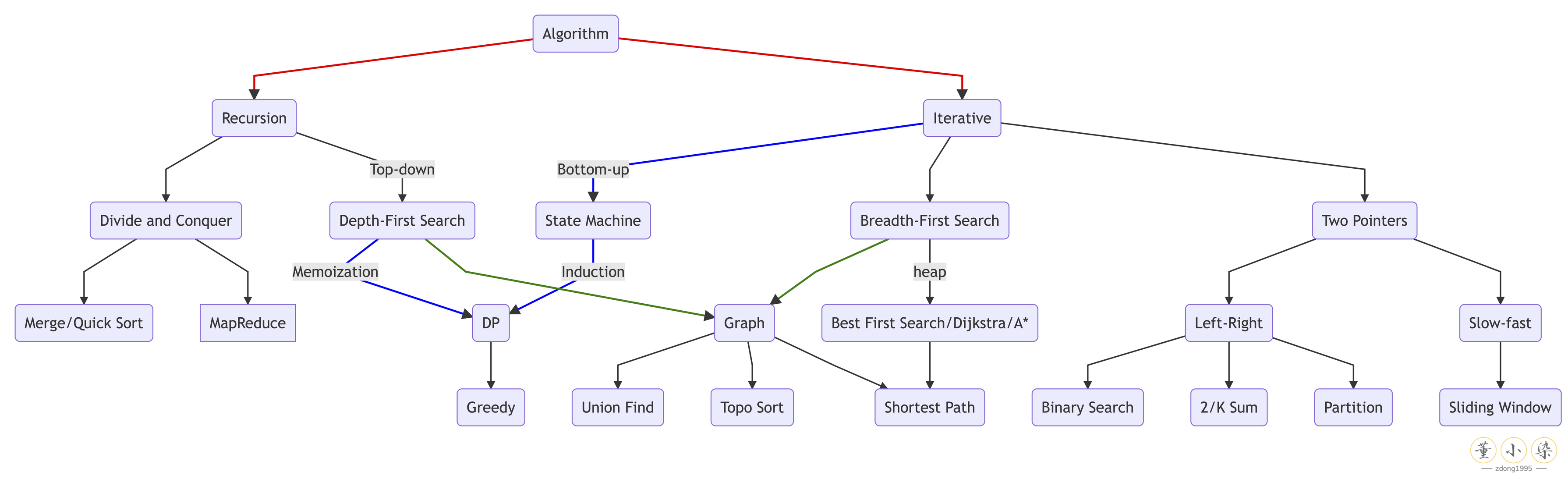
3. 算法的学习方法论

和数据结构一样，Top-down 来看算法可以分为两种：基于迭代和基于递归的算法。

Recursion

在我看来，对于转专业的我们来说，最重要的是前期 Recursin 思维的养成。在没有入门递归的时候，我们往往看到一个 solution 会惊讶『这怎么就三四行代码，怎么做到的』。但是等学会递归后，会发现这是一个很精巧且非常直觉化的一个算法思路，而且 Recursion 也是 DFS 算法的基础核心。

Recursion 是什么？

递归是一种 Top-down 的思考方式，本质是将大问题不断细化为小的子问题。当解决了子问题后，再利用子问题的结果来解决大问题。

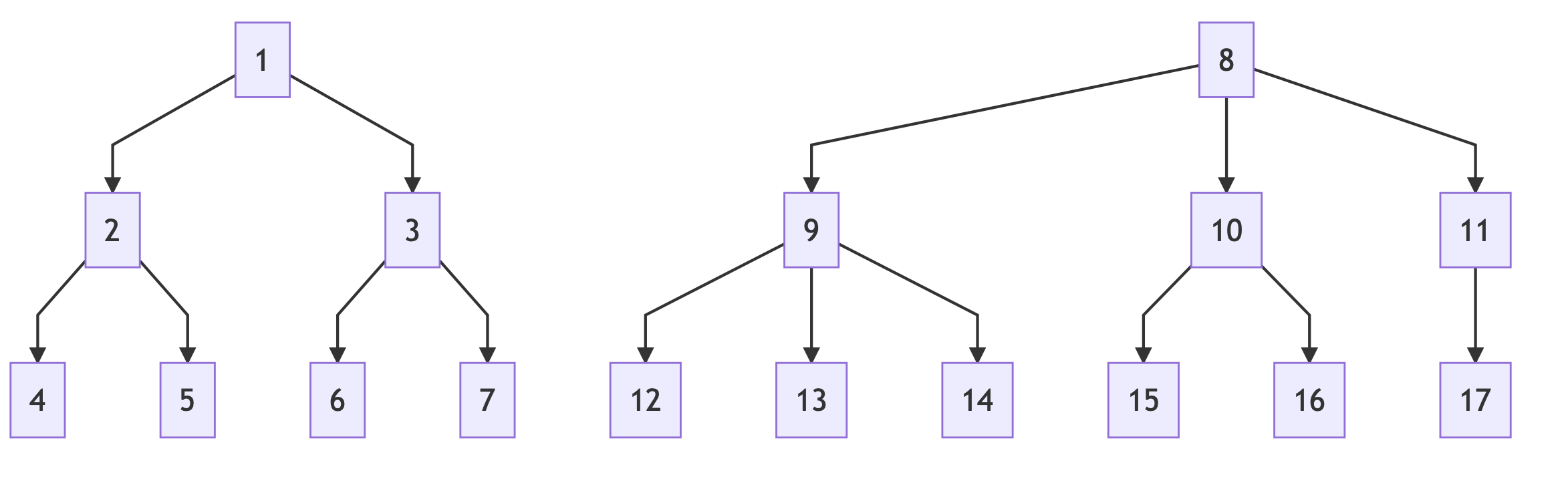
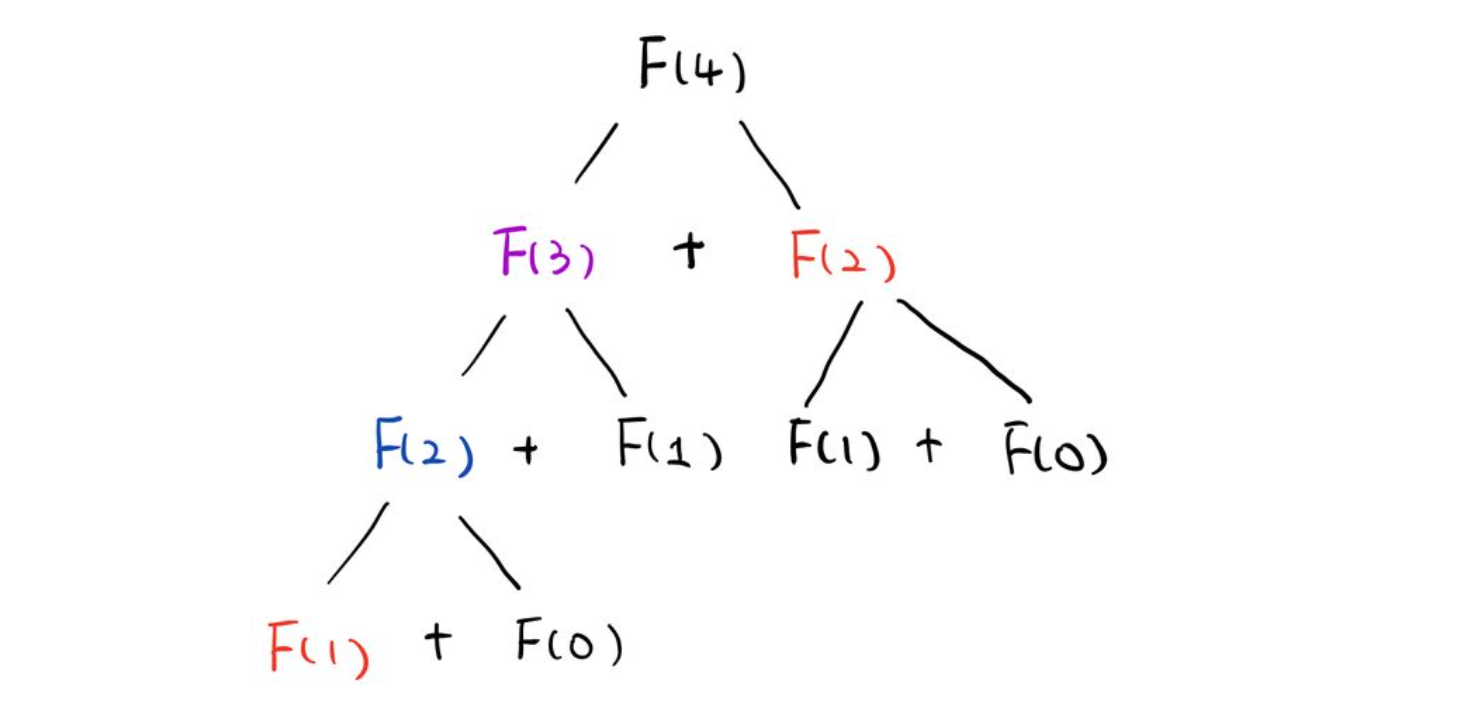
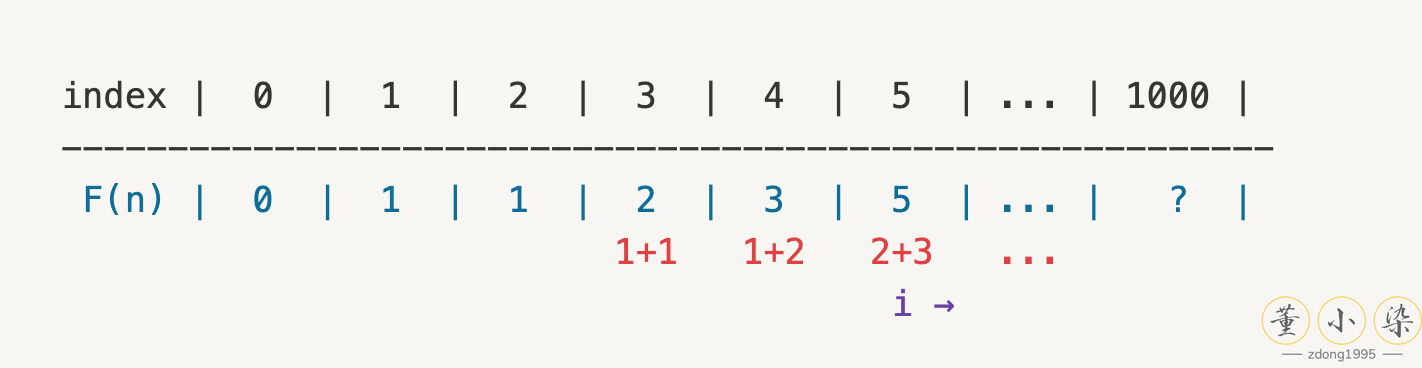
如对于 Fibonacci 问题，我们想要得到 $F(4)$，就需要知道 $F(3)$ 和 $F(2)$，而想要知道 $F(3)$ 就又需要 $F(2)$ 和 $F(1)$。这样可以逐层缩小问题的 size，从 4 一直 boild down 到 $F(1)$ 和 $F(0)$。因此可以得到下图的 Recursion Tree：

Tree 这种数据结构就是一个 Recursive 结构，也因此大多数的 Tree 相关的问题都可以通过 recursion 来轻松求解。在算法学习的刚开始，强烈建议多做一些 Tree 的题目来培养自己的 Recurison 思维。

DFS

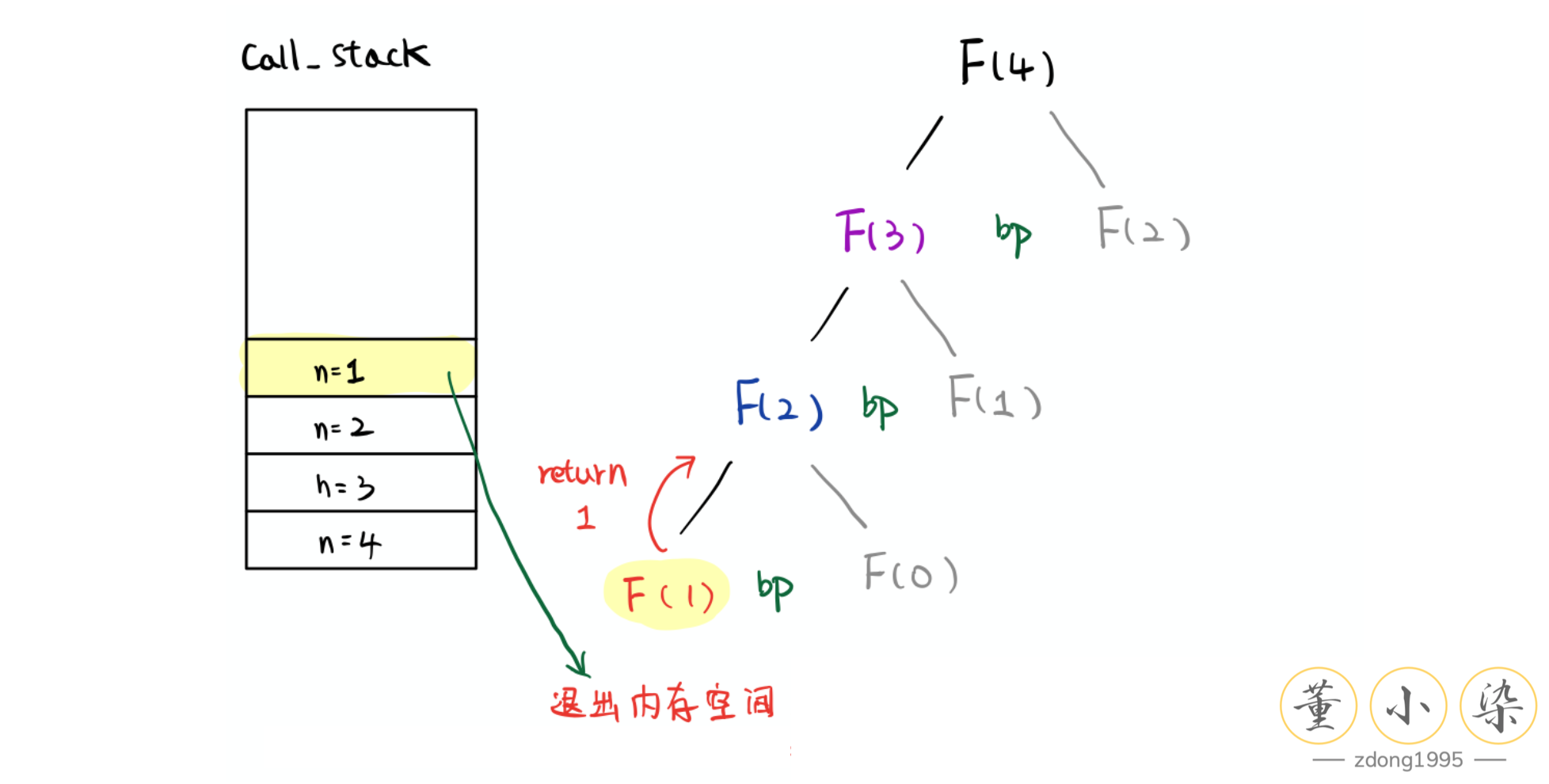
在实际运行过程中，Recursion 是深度优先 Depth-First 的，也就是会一头扎到底，即『递』的过程，直到问题不能再缩小。解决完最小的子问题后，再 return 到上一层，即『归』的过程。有递有归，才能不断地将 subproblem 的结果进行不断地计算操作，最终得到原始规模的问题的结果。

可以看到 Recursion 实际上就是对我们所画出来的 Recursion Tree 的一个遍历过程，也就是 Tree 上的 Depth-First Search。推广来看，对于 DFS 算法来说，基本都是对 Recursion Tree 的遍历，只不过分叉数不一样，在这里我们只有两个分叉，但是对于图可能会是多叉树。

因此，DFS 算法可以用于各类搜索问题，不仅限于 Graph 和 Tree，对于一些问题可以根据内部关系转换为隐式图，从而通过 DFS 搜索隐式图得到结果，也可以搜索 State 来得到结果。经典的 Subset，Permutation，Cominbation 都可以通过 DFS 来转换为对 Tree 的遍历进行解决。

Divide and Conquer

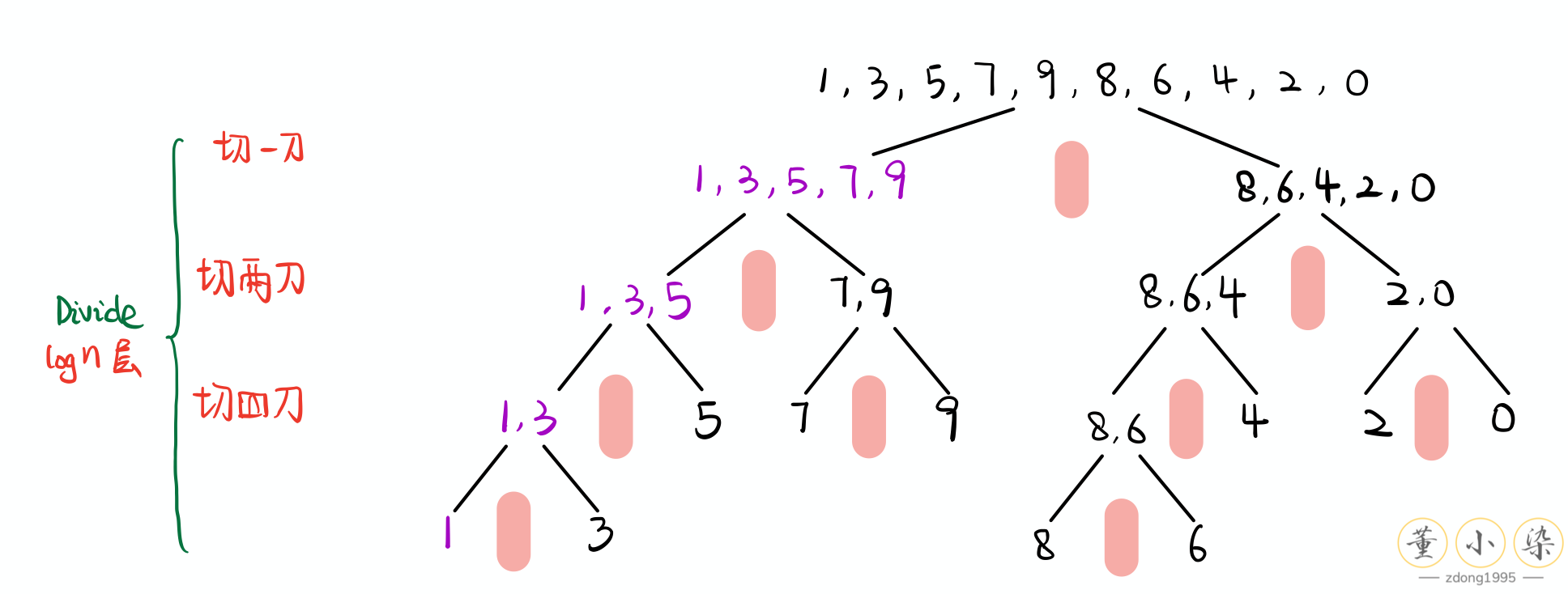
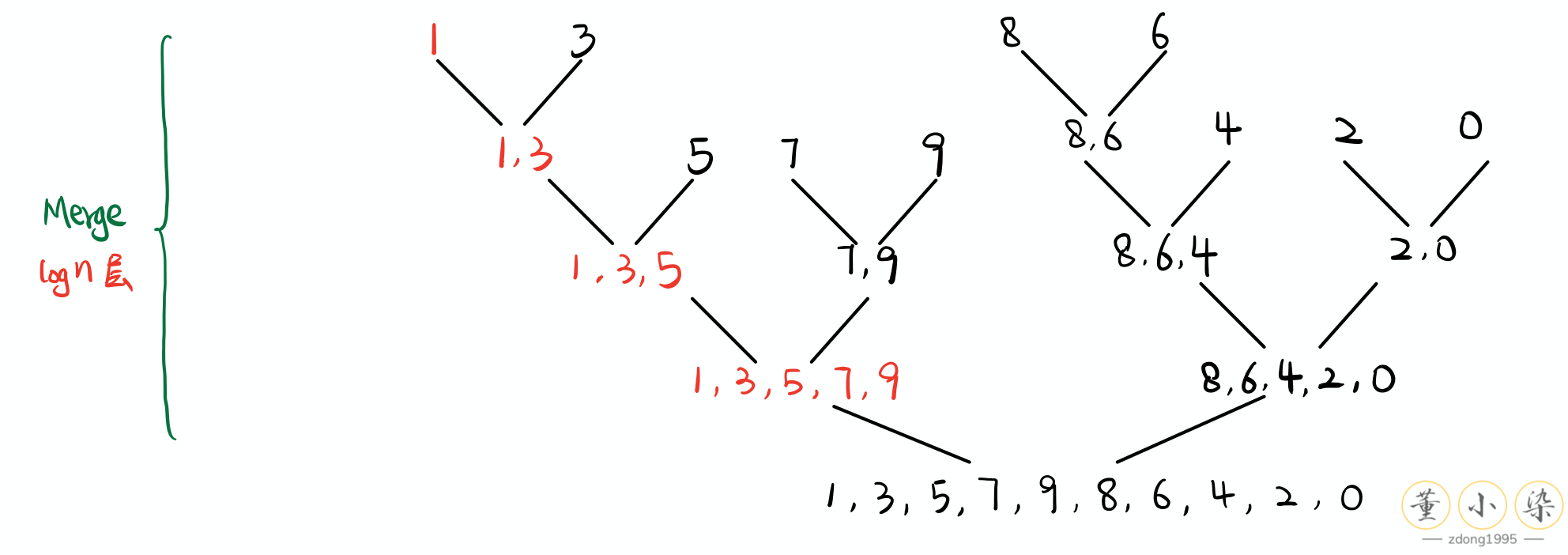
Recursion 的重要应用就是 Divide and Conquer 『分而治之』，将大问题分成小问题进行解决，之后才将两个小问题的结果合并起来。而这个过程需要用到 Recursion 来实现。如最经典的 Merge Sort 问题，我们需要排序一个数组，如果我们可以将左边排序，将右边排序，将两边合并起来即可。对于每一个半边，我们又可以再继续切开进行分别排序，最后可以将问题的 size 缩小到 1。

等到我们划分到最小问题后，再分别进行排序处理，再合并起来，就得到了需要排序的次小问题的结果。逐层操作，依次 return，最后回到初始层得到最终的结果。

如果问题规模非常非常大，一台电脑都无法装下呢？这时候就有 MapReduce 算法出场了，和 Merge Sort 一样，不过我们分开的工作会发送到不同的电脑进行计算，分别得到结果后再合并结果，用于分布式系统的并行处理。

Iterative 实现

和 Recursion 相对的，就是 Iterative 迭代实现的算法。一般来说就是循环进行计算，每一次循环利用上一次迭代计算得到的结果来得到新的结果。

1
2
3
4
5
6

public int getSum(int[] arr) {
  int sum = 0;
  for (int i = 0; i < arr.length; i++) {
    sum += arr[i];
  }
}

上述代码就是一个最简单的迭代算法，不断迭代遍历整个数组求得整个数组的和。实际中我们迭代算法更多地通过双指针 Two Pointers 方法一个一个遍历操作，或通过 Breadth-First Search (BFS) 宽度优先搜索一层一层遍历操作。

Two Pointers

双指针原则上不是一个算法，只不过是一种技巧，广泛使用于解决 Array，LinkedList 及 String 的题目。

• 相向双指针：如 2 Sum 一大类问题，Partition 问题，Quick Sort 中每次将数组分成两段就是利用这个技巧
• 同向双指针：Fast-slow 双指针解决一类 LinkedList 的问题，Array 及 String 的 Deduplication 问题及修改问题
• K 个指针：解决一类 Kth element 及 K-way merge 类问题
• 滑动窗口：Sliding Window 是一种高级的同向双指针技巧，通过维护左右指针间的窗口，可以解决一系列子串问题等

Binary Search

同时 Binary Search 二分搜索也是一种双指针技巧的变种，类似 Divide and conquer 的过程，但是只是在每次减小一半的搜索范围。如果我们发现目标不在我们范围内，就去搜索另外一半，逐层迭代，最后找到结果。对于已经排序好的 input，往往需要向 Binary Search 的思路进行思考。

BFS

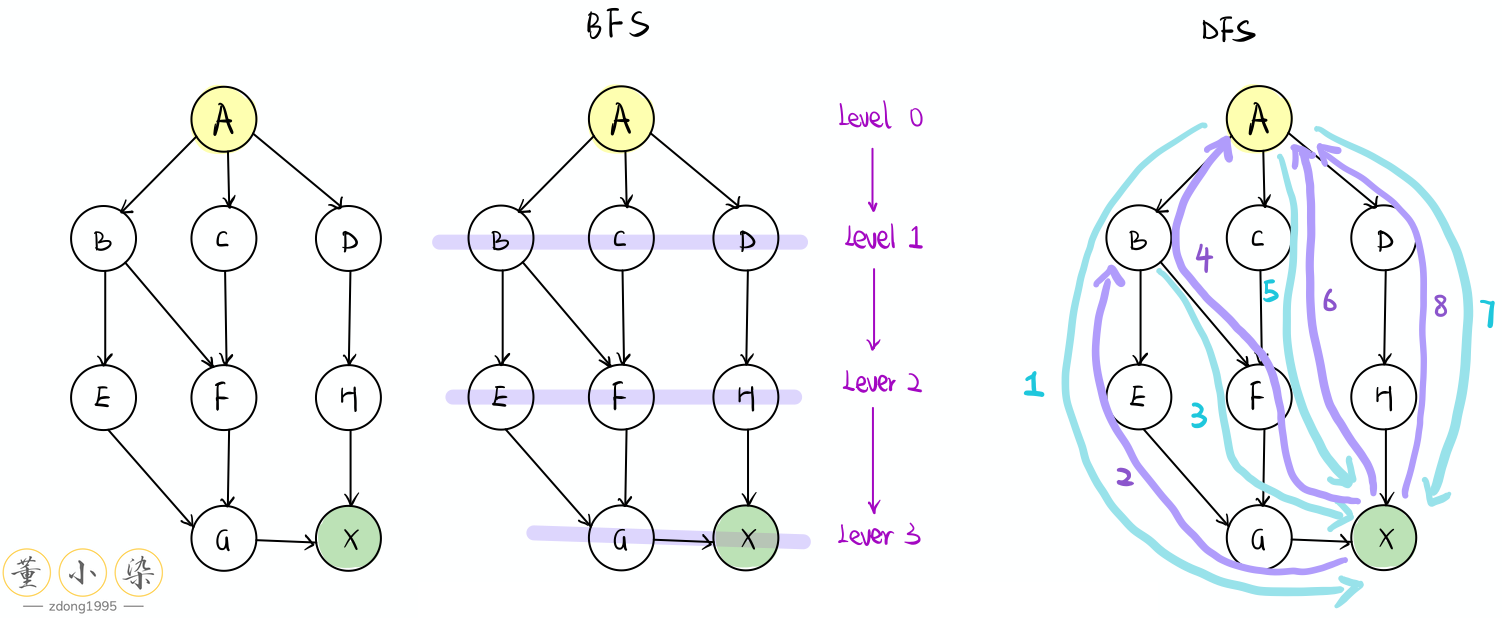
Breadth-First Search 算法是广度优先，逐层遍历操作。和 DFS 不同，DFS 是找准一个方向，『不撞南墙不回头』，先『递』再『归』。BFS 是『雨露均沾』，将自己周围距离相等点都先遍历，将一层处理完后再下一层。BFS 是一种更大规模的 Iterative 的算法，需要使用队列结构来维护我们的层级结构。

BFS 一般适合于解决最短路径问题，由于它『雨露均沾』的特性，它在每一层将下一层的元素都遍历了一遍，所以当 BFS 第一次遍历到目标元素的时候，即为最短路径。

BFS 另一大重要考点是 Topological Sort，同时 BFS 还有 Best First Search，Dijkstra 等针对复杂图的优化算法。BFS 这类算法每次运行完后都可以得到由出发点到所有 reachable 的点的最短距离，即**『点到面』的距离**。

Dynamic Programming

最后我们来聊聊动态规划。还是一样的出发点，Recursion 和 Iterative。在 DFS 中我们会尝试搜索所有可能的路径，solutions，或者说 states。

继续以 Fibonacci 为例，我们将整个 Recursion tree 遍历了一遍，得到了最后的结果，但是可以发现过程中有很多重复操作，我们已经求过 $F(2)$ 的结果了，后续就不需要再跳入 Recursion 再计算一次了。因此可以使用一个 Table 来记忆化我们的结果，从而将 DFS 进行剪枝得到最后的 solution。这样的思路，我们从 Top-down 出发进行 DFS，再使用 Memoization 优化得到的结果，就是动态规划。我们只是将一些中间的 states 通过空间存储了下来，从而加速跳过后续的一些 states。这也是空间换时间的常用做法。

另一种动态规划是基于 Iterative 的思路，类似于我们以前所学过的数学归纳法。把一个大问题的解决方案用小的问题（们) 来解决，也就是思考从问题 size = n-1 增加到 size = n 的时候, 如何用小问题的 solution构建大问题的solution，即 Bottom-up 从小到大处理问题。也就是说我们直接 dive 到最小的问题，解决后得到 initial state，再依次 iterative 地计算得到 intermediate state，最终得到 final state 的答案。

因此可以看到，动态规划有两种思考思路，但是核心都是 Memoization 通过子问题的 solution 来解决大问题。动态规划的关键是 states 的记录与搜索，多个 states 叠加最终得到我们的 final state。

4. Summary

可以看到，其实数据结构和算法都是有迹可循的体系。从一维入数据结构手，从 LinkedList 开始学习 Iterative 和 Recursion。前期主要为了培养递归思维，从 LinkedList 到 Tree 进行 Recursion 的练习，同时学习 Two Pointers 的操作技巧。这时恭喜你，你可以非常清晰得想明白并轻松手写排序算法了。后续就是大规模的 Search 练习，BFS，DFS，二分搜索，剪枝，记忆化，优化。等这些基本功扎实后，再去接触高级算法和数据结构，提升综合实力。

欢迎关注我的微信公众号『董小染』。