一题顶四题，一道题掌握 LinkedList 的 Iterative

首先复习一下在之前的文章半年零基础做完 300 题，我的算法与数据结构学习方法论中，我们提到的 Linked List 的结构：

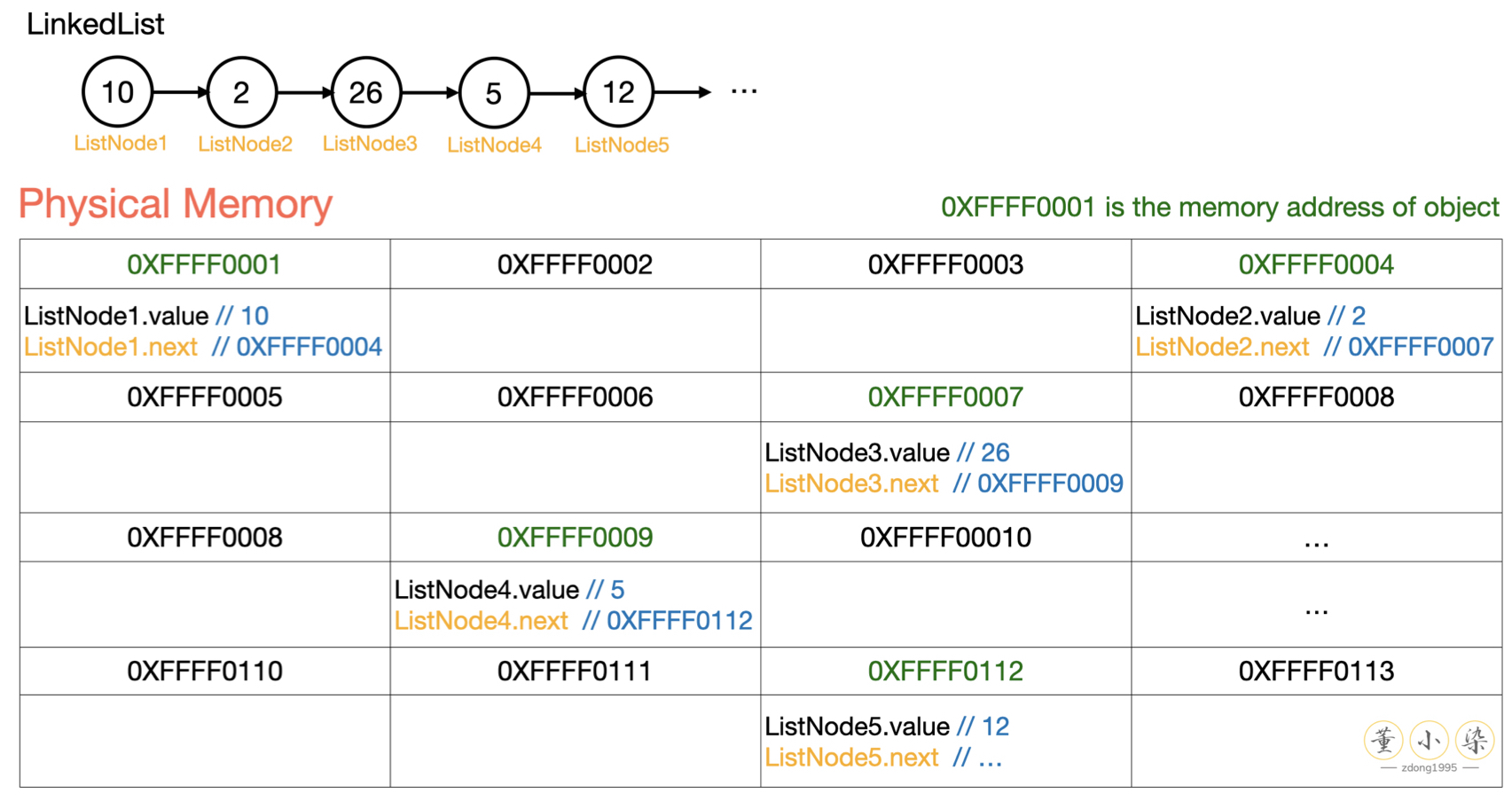
LinkedList 是在逻辑上连续的数组，但是在物理地址上并不是像 Array 一样连续的。LinkedList 包含一系列 ListNode：

1
2
3
4

class ListNode {
  int val;
  ListNode next;
}  

每一个 Node 有一个 next 的 field 存储下一个 Node 的引用地址，因此可以顺着当前 Node 找到下一个 Node。因此可以将 LinkedList 类比为『一堆箱子』，每个箱子里存放的是元素和下一个箱子的名片。

由此我们可以发现 Linked List 的两个重要的注意点：

• Linked List 都是以 head 来给定，相当于我们从 head 出发，沿着 next 地址一路找下去，可以找到 Linked List 的末尾。因此对于 Linked List 来说，我们始终要保持有 head 地址的控制权。
• 在找 next 的时候，我们通过 node.next 来得到下一个 Node 的地址。由于 next 本身就是一个 ListNode 类型的 reference，在 invoke node.next 时相当于我们对 node 这个 reference 地址进行了 dereference，即『通过名片找到对应的箱子』。如果这个 node 即『名片』本身就是一个 Null，那么对 Null 进行 dereference 就会发生 NullPointerException。因此在进行 dereference 前一定要先 check 当前地址对应元素是否为 Null。

下面我们以一道 Medium 的题目来一穿四解决 4 道 Linked List 的题目，来掌握 Iterative 操作的技巧。

LC143: Reorder List

Given a singly linked list $L: L_0→L_1→…→L_{n-1}→L_n$,

Reorder it to: $L’: L_0→L_n→L_1→L_{n-1}→…$

You may not modify the values in the list’s nodes, only nodes itself may be changed.

首先拿到题目后先理清题意，我们需要将一个给定的 Linked List 首尾交错连接起来，将第 1 个和第 n - 1 个连接，接下来是第 2 个和第 n - 2 个，以此类推。

乍一看好像没什么好的思路，因为对于 Linked List 我们需要从 head 向后找 next 才能进行遍历。没有特别 intuitive 的思路时，我们可以画图来分析下：

可以看到原来的 List 好像分成了两块，然后蓝色的部分和反过来的红色部分交错连接了起来。那么顺着这个发现我们可以自然而然想到一个思路：

• Step 1：找到 Linked List 的中点
• Step 2：Reverse 第二部分 sublist
• Step 3：将第一部分 sublist 和第二部分交错 merge 起来

在上一篇文章 当我们谈论刷题时，到底在刷什么 中提到了我们思考时可以记录下我们的 trajectory，因此可以先在我们的 function signature 中先 markup 一下：

1
2
3
4
5
6
7

public void reorder(ListNode head) {
  // find middle node of linkedlist
  
  // reverse second sublist
  
  // merge two sublists and return
}

由于我们的 Method reorder 的主逻辑就是为了进行 reorder list，因此我们可以将这三部分提取出来作为单独的 helper function，最后将 3 个积木搭起来就可以得到最后的结果了。因此我们需要考虑这三个 helper function 的 API 的接口应该如何设计：

findMiddle()

findMiddle() 的 input 应该是一个 Linked List，即一个给定的 head。由于 method 的定义就是为了找到 middle node，因此 output type 也自然而然应该是一个 ListNode。

下面来考虑一下该 API 的功能定义，我们如何定义『Middle』。对于奇数 (2n+1) 个 Node 的 list 自然而然是第 (n+1) 个，但是对于偶数 (2n) 个 Node 时，我们应该 return 第 n 个还是第 n + 1 个 Node 呢？

对于结果来说其实这两个结果都没有太大影响，但是当我们实际 implementation 时，return 第 n 个即 middle 靠左的 Node 的会更加方便一点。因为实际在操作过程，我们 Reverse 了第二部分 list 后，我们将两部分一个一个 merge 起来时，如果没有将第一部分的最后一个 node （即 3）和下一个 node （即 4）进行断开的话，最后得到的结果是会形成环的。后面 implementation 我们会讨论一下细节，因此在这里对于偶数个数的 nodes 我们得到 middle 靠左的 node 会更加方便。

由此可以得到我们 findMiddle() 的 API 接口定义：

1
2
3

private ListNode findMiddle(ListNode head) {
  // find the middle (leftside) of given list
}

reverse()

同理对于 reverse 过程我们的的 input 应该是一个 Linked List，即一个给定的 head。对于 output 我们应该是 void 还是 ListNode 呢。因为后续我们的 merge 操作一定是从两个 sublist 的 head 开始进行的，因此我们也是需要 return 一个 ListNode。因此得到 reverse() 的 API 接口定义：

1
2
3

private ListNode reverse(ListNode head) {
  // reverse list and return new head
}

mergeList()

最后，由前面的步骤我们可以得到 merge 过程的 input 是两个 Linked List，即两个 head。由于我们的 reorder() 主逻辑 API 没有 return，进行 in-place 操作，因此需要将原来的 head 替换成新的 newHead，因此我们 output 需要返回 merge 后得到的 new head。因此得到 mergeList() 的 API 接口定义：

1
2
3

private ListNode mergeList(ListNode one, ListNode two) {
  // merge two list and return new head
}

这样我们根据定义的 API 接口可以完善我们的主逻辑，之后就可以 dive into 每一个 helper function 如何实现了。需要注意的是因为我们 middle 找的是 middle 偏左的 node，因此我们 reverse() 的 input head 是 mid.next。在完成 reverse 后我们就不需要保持 mid 到 mid.next 的连通了，及时 delink 避免成环，省得后续 debug 死循环发懵。

1
2
3
4
5
6
7
8
9

public ListNode reorder(ListNode head) {
  // find middle node of linkedlist
  ListNode mid = findMiddle(head);
  // reverse second sublist
  ListNode secondHead = reverse(mid.next);
  mid.next = null; // delink to avoid cycle
  // merge two sublists and return
  return mergeList(head, secondHead);
}

这样我们就逐个击破就好了，正好你可以顺手在 LeetCode 将子问题都 AC 了。

LC876: Find the middle node of Linked List

Given a non-empty, singly linked list with head node head, return a middle node of linked list.

If there are two middle nodes, return the second middle node.

这道题目和我们的需求基本一致，只不过它对于偶数个 Node return 的是靠右的一个。不过都大同小异，分析清楚即可。这里我们会利用到一个小技巧，『快慢双指针』，后面双指针部分我们也会详细介绍同类型题目。

同向快慢双指针的思路就和小时候小学数学题一样，小明每小时跑 10 公里，小红跑 5 公里，求问小明到达终点时，小红在什么位置？自然而然小红会在中点位置。

对于 Linked List 来说，每次快指针走两步，即 fast = fast.next.next，慢指针走一步，即 slow = slow.next。最后快指针到达末尾时，慢指针在中间。这里最 tricky 的部分就是如何定义 termination condition，这也是 iterative 最需要注意的地方。

对于奇数个 Node 的终止情况如下：

对于偶数个 Node 的终止情况如下：

• 左 mid：第 $n$ 个 node → 慢指针需要走 $(n-1)$ 步，快指针走了走了 $(n-1)$ 步到达第 $(2n-1)$ 个 node，即最后一个 node 前一个 node fast.next.next == null

• 右 mid:第 $(n+1)$ 个 node → 慢指针需要走 $n$ 步，快指针走了 $n$ 步到达第 $(2n+1)$ 个 node，即*最后一个 node 的 next node (null) ⇒ fast == null

因此我们很轻松写出代码：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

public ListNode findMiddleRight(ListNode head) {
    if (head == null) {
        return null;
    }
    ListNode fast = head;
    ListNode slow = head;
    
    while (fast != null && fast.next != null) { 
			  // even && odd, fast != null 先判断
      	// 如果为 false 则不会进行后面的判断，不会触发 NPE
	      fast = fast.next.next;
	      slow = slow.next;
    }
    return slow;
}

找 middle 靠左只需要修改退出条件：

1
2
3

while (fast.next != null && fast.next.next != null) {
  	// odd && even
}

Time Complexity: $O(N)$ ，我们需要遍历整个 list 所有 nodes

Space Comlexity: $O(1)$，没有任何额外数据结构和 call stack 的使用

LC206: Reverse Linked List

Given a singly linked list $L: L_0→L_1→…→L_{n-1}→L_n$ Reverse it to: $L’: L_n→L_{n-1}→…→L_1→L_0$

这道题目也是非常基本功的面试题目，在这部分我们先讲解 Iterative 的做法，后续 Recursion 时再分享 Recursive 的思路。

我们在第一篇文章中就讨论了『算法的核心是改变 state』，因此这里我们可以根据 state 如何改变来设计我们的算法。首先来看一下 reverse list 的过程中发生了什么，对于 list 中的每一个位置都发生了 reverse，因此最终我们原始 head 会变成最终的 tail，原始的 tail 会变成新的 head。因此我们可以思考从头到尾 iterative traverse 一遍，过程中依次翻转，最后停在最后一个 node，也就是我们的 newHead。那么每一次翻转需要经过哪几个 states 呢？

和之前的 findMiddle() 一样，我们 traverse Linked List 仍然需要指针来进行操作。只不过两个指针不够，需要一个临时指针来存储下一个 node，否则完成当前位置的翻转后就无法继续 traverse 下去。因此 reverse 过程也非常直接，prev 初始化为 Null，因为第一个 Node 最后会成为最后一个 Node，最后一个 Node 的 next 是 Null。之后依次进行翻转，由于已经将 cur.next 存储在 next 中，可以放心地切断 cur 与 next 的连接，再将 cur 的 next 指向 prev 即可。再整体顺移到下一个 iteration 继续进行相同的操作，从而可以从左向右翻转整个 Linked List。那么问题来了，和上一道题目一样，我们的 terminate condition 是什么？

可以看到最终翻转完最后一个 Node，结束最后一个 iteration 后，cur 停在了 Null，而 prev 停在了最后一个 Node。因此最终 prev 是我们的 new Head，terminate condition 是 cur == Null。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

public ListNode reverseLinkedList(ListNode head) {
  if (head == null || head.next == null) {
    return head;
  }
  ListNode cur = head;
  ListNode prev = null;
  ListNode next = null;
  while (cur != null) {
    next = head.next;
    cur.next = prev;  // reverse step
    // move to next position
    prev = cur;
    cur = next;
  }
  return prev; // 最终 prev 为 head
}

Time Complexity: $O(N)$ ，我们需要遍历整个 list 所有 nodes

Space Comlexity: $O(1)$，没有任何额外数据结构和 call stack 的使用

LC21: Merge Two Sorted Linked List

Merge two sorted linked lists and return it as a sorted list. The list should be made by splicing together the nodes of the first two lists.

这道题目比我们这里的需求稍微复杂一些，我们 helper function 只需要一个接一个 merge 即可，这道题目需要比较两个 Node 的值，先 Merge 小的，但是原理都是相通的。

这里需要用到的小技巧是 dummy node。当我们需要不断地将新的 Node append 到一个空的 Linked List 时，由于我们没有一个 initial head，如果通过 corner case 处理进行比较两个 List 的 head 再去选择 result list 的 head 时会显得过于麻烦。如果不是两个 List，是 k 个 List 就会更加麻烦，因此可以使用 dummy head 来简化逻辑。

我们通过创建一个 dummy head，再依次不断的将 Node 来 append 到 dummy 的后面，我们最后实际的 head 就是 dummy.next。

Merge 完成后的结果：

要注意的是，由于我们是 in place 在原来的 node 上面操作，semantically 来看我们是把一个 node 连接到了尾部，但是实际上 physically 我们是把整个 list 都链接到了后面。只是『在我们脑海中』，我们思考是把 dummy 和 cur 之间的考虑为我们 merge 后的 list。在实际操作过程中，semantically 想象中的 list1 ，list2 ，mergedList 其实 physically 都是同一个链表，只是不同的 head 区分了不同的想象对象。记住这一点以后，对于避免成环和 post processing 就会更加明了。

在我们的 implementation 中，由于要不断在末尾添加新的元素，因此 maintain 一个 tail 指针会帮助我们更方便地处理。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
  ListNode dummy = new ListNode(0);
  ListNode cur = dummy; // maintain as tail
  // iterative until we traverse to the end to one linked list
  while (l1 != null && l2 != null) {
    // compare to select the smalled one node to connect to tail
    if (l1.val < l2.val) {
      cur.next = l1;
      l1 = l1.next;
    } else {
      cur.next = l2;
      l2 = l2.next;
    }
    cur = cur.next; // update tail
  }

  // out of loop condition: l1 == null or l2 == null or both are null
  if (l1 != null) {
    cur.next = l1; // connect the non null one to tail
  } else {
    cur.next = l2; // what ever l2 == null or l2 != null
  }
  return dummy.next; // dummy.next will be the new head
}

Time Complexity: $O(M+N)$，我们需要遍历两个 list 所有 nodes，M 和 N 分别为两个 list 的 node 个数

Space Comlexity: $O(1)$，没有任何额外数据结构和 call stack 的使用

LC143: Reorder List

回到我们的原题目，所有的 helper function 都已经实现完毕，我们就可以很轻松拼接起来完成题目啦。这里的 Merge list 比上一题更加简单，都不需要进行比较大小，而且 else { cur.next = two; } 也可以不写，因为不会出现这种情况。

因为在找到中间节点以后，我们就把 middle.next 赋值给了第二半作为头节点，这样的话在总节点数为偶数的情况下，两半节点数是一样的，总节点为奇数的时候前一半会多一个节点。也就是说在这种 merge 操作的情况下，第二半 list 永远不会有剩余的元素 。唯一可能有剩余元素的情况也只会出现在前一半 list 里。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64

public void reorderList(ListNode head) {
  if (head == null || head.next == null) {
    return;
  }
  // 1. find the mid node of list
  ListNode mid = findMid(head);
  // 2. reverse the second part
  ListNode reversedMid = reverseList(mid.next);
  mid.next = null; // de-link mid to the second part to avoid potential cycle
  // 3. merge with first part
  ListNode newHead = merge(head, reversedMid);
  head = newHead;
}

private ListNode findMid(ListNode head) {
  /*
   * return the mid node of linked list (first mid for even number)
   * odd 2n+1 : slow n+1, fast 2n+1
   * even 2n : slow n, fast 2n-1
   * assumption : head != null && head.next != null
   */
  ListNode slow = head;
  ListNode fast = head;
  while (fast.next != null && fast.next.next != null) { // odd case && even case
    fast = fast.next.next;
    slow = slow.next;
  }
  return slow;
}

private ListNode reverseList(ListNode head) {
  if (head == null || head.next == null) {
    return head;
  }
  ListNode prev = null;
  ListNode cur = head;
  while (cur != null) {
    ListNode next = cur.next;
    cur.next = prev;
    prev = cur;
    cur = next;
  }
  return prev;
}

private ListNode merge(ListNode head1, ListNode head2) {
  ListNode dummy = new ListNode(0);
  ListNode tail = dummy;
  // traverse head1 and head2 to add nodes to tail one by one
  while (head1 != null && head2 != null) {
    tail.next = head1;
    head1 = head1.next;
    tail.next.next = head2;
    head2 = head2.next;
    tail = tail.next.next;
  }
  // out of loop condition:
  // odd: head2 == null but head1 != null -> tail connect to head1
  // even: head1 == null && head2 == null -> no need to do
  if (head1 != null) {
    tail.next = head1;
  }
  return dummy.next; // dummy.next is the real head
}

Time Complexity: $O(N)$ ，我们无论是 reverse 还是 merge 还是 findmid 都是操作的是 list 的所有 nodes，只不过相当于遍历了 3 次

Space Comlexity: $O(1)$，没有任何额外数据结构和 call stack 的使用

Summary

最后我们来看看为什么会成环:

因此在我们找到 mid 后，当 mid.next 已经 reverse 完毕，就需要及时 delink，否则后续我们往往会忘记。

OK，今天我们通过这一道题目来解决一套题目。可以看到 Linked List 的操作其实非常简单，Itrative 操作时需要使用指针进行 traversal，无论是 cur 和 prev 还是 slow 和 fast，在操作时都需要注意下面几点即可省去你大量的 debug 时间：

• derefrence 前一定要先 check 该 Node 是否为 Null
• 不能边操作边丢失了 head，否则就找不到当前的链表了
• 写 while 循环 traverse 时一定要明确 termination condition
• 当我们向初始为空的 LinkedList 插入元素或者不清楚哪一个 node 才是 result 的 head 的时候，可以使用 dummy node 来优化 corner case 处理
• 如果在 LinkedList 尾部需要不断地添加元素，可以 maintain 一个 tail 指针便于操作

光看不练等于没见

趁热打铁，快去解决今天的题目吧：

• LC143: Reorder List
• LC876: Find the middle node of Linked List
• LC206: Reverse Linked List
• LC21: Merge Two Sorted Linked list

最后，如果这篇文章讲解对你有所帮助，欢迎分享给需要的人。谢谢！

欢迎关注我的微信公众号『董小染』。