Tree 还可以这样 O(1) 空间遍历？四题带你深入理解 LinkedList 与 Tree 的关系

相信大家都听过说二叉树的 PreOrder 先序遍历，PostOrder 后续遍历，InOrder 中续遍历，今天我们来接着上一篇文章的 Linked List 遍历，提供一个新的遍历方式，通过这个视角来深入理解一下一维数据结构与二维数据结构 Iterative 的关系。

在 半年零基础做完 300 题，我的算法与数据结构学习方法论 我们介绍了一维 LinkedList 的 Iterative 操作和技巧，在一题顶四题，一道题掌握 LinkedList 的 Iterative 中我们也讨论了二维数据结构 Tree 和 Graph 都是由 LinkedList 衍生而来。将一维数据结构 LinkedList 将箱子里的『名片』从一张名片变成『多张名片』，那么就得到了非线性的数据结构 Tree 和 Graph。今天我们就来看看这最基础的二维数据结构，二叉树 Binary Tree 如何顺此思路进行 Iterative 操作。

Tree 和 LinkedList 的关系

ListNode vs. TreeNode

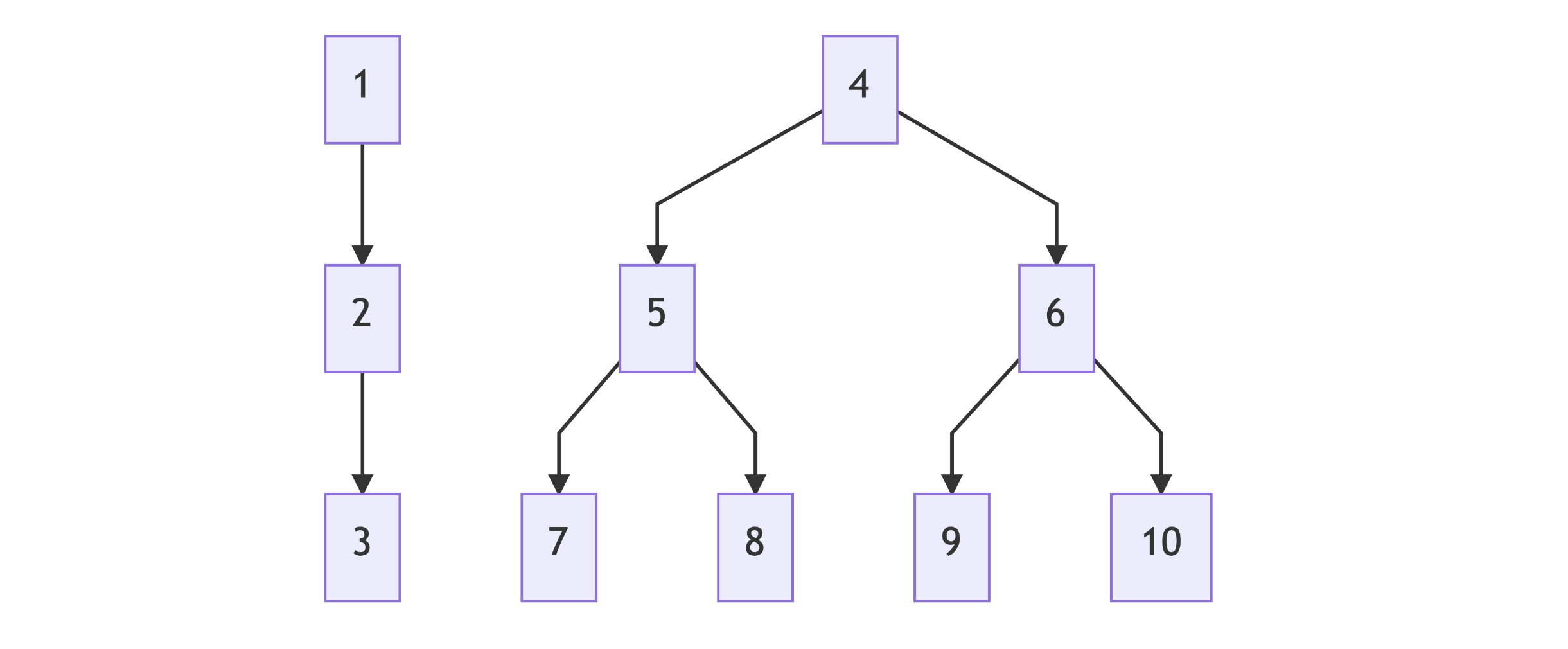
我们已经知道，对于 Linked List，每一个 ListNode 存储 val 和下一个 ListNode 的地址next 。那么对于常见的二叉树 Binary Tree，每一个 Node 最多有两个孩子，因此其中 TreeNode 也就只需要多存储一个地址即可：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

class ListNode {
  int val;
  ListNode next;
}  

class TreeNode {
  int key;
  TreeNode leftChild;
  TreeNode rightChild;
}

• ListNode 存一张名片：下一个箱子的名片
• TreeNode 存两张名片：左孩子的名片和右孩子的名片

Linked List vs. Tree

如果我们还是按照以前 Bottom-up 自底向上进行思考，可以发现链表和树就是一个 generalization 的过程。

• 对于 LinkedList ，其实就是一个一叉树，可以认为不分『左孩子』和『右孩子』，只有孩子 next。
• 对于 Binary Tree，是从一到二的过程，我们有了『左孩子』和『右孩子』，也就是说，每一个 Node 最多可以连接两个其他 Node，最少什么都不连接。
• 对于 K-nary Tree，就是从二到多的过程，泛化出来一堆孩子，因此我们选择用一个 List 进行存储每一个 Node 连接的其他所有 Children Node。

但是，无论是 LinkedList，还是 Binary Tree，还是 K-nary Tree，都需要注意的点是只有一个 source node，而且没有环。如果有环，或者多个源点，那么就成了 Graph。

Binary Tree = Multilevel Linked List

在前面的分析中，我们发现了，无论是叫 next，还是 left 或 right，都只是一个符号式的语言来 identify 我们存储的 node。因此对于链表我们称下一个 node 为 next，也可以称下一个为 left，这些都无所谓，只不过这些约定俗称的名字可以帮助我们实现 semantic 和 implementation 的统一而已。

但是正因为这些名字无所谓，如果抛开这些左右的概念，我们对二叉树可以有另一种认识：

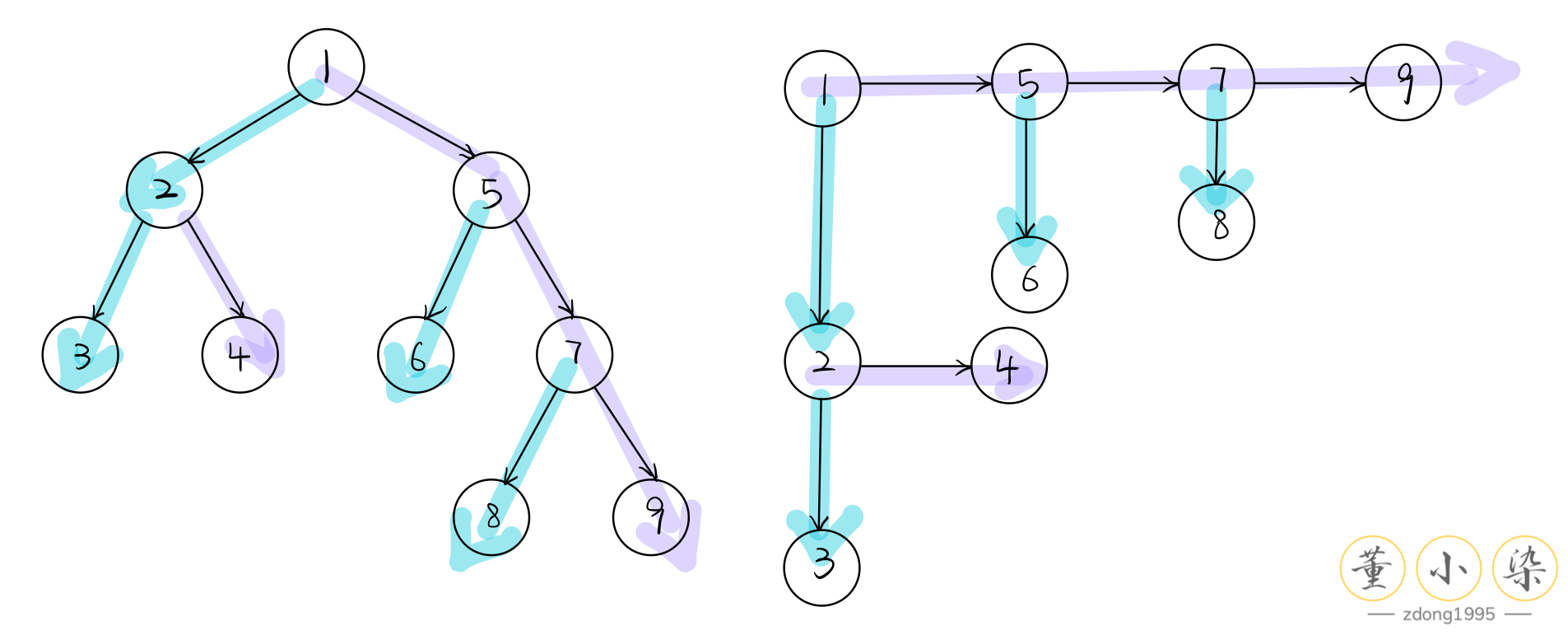
其实二叉树就是一个由『一路向左』或『一路向右』的 Linked List 串起来的多层链表结构，如果将 Binary Tree 旋转 90 度，可以发现这时候的 left 和 right 就没有什么意义了，这时候的 right 就像是 Linked List 中的 next，left 就变成了 down 或者 child 的语义，反之亦然。

在我们掌握了 Linked List 的 itrative 过程后，我们也就自然而然可以将一维的 iterative 来泛化扩展到二维的 iterative 过程。今天我们用两个类型，四道题目来深化一下理解。

Iterative 操作二叉树有各种方式，如利用 stack，queue 等进行操作，今天我这里分享的是更省空间的没有任何额外空间的 in-place iterative 方法，同时可以很好练习我们对于二维数据结构的理解。

PS: 以下题目均可以使用 Recursion 解决，但是这里我们只讨论这种由 Linked List 的遍历衍生思考出来的这种遍历方式来 Iterative 解决，后续 Recursion 章节我们再回过头来讨论如何进行递归求解。

Tree 的 Iterative『伪逐层遍历』

下面来看一道题目 LeetCode 114: Flatten a Tree to Linked List

Given a binary tree, flatten it to a linked list in-place.

For example, given the following tree:

1 2 3 4 5

1 / \ 2 5 / \ \ 3 4 6

The flattened tree should look like:

1 2 3 4 5 6 7 8 9 10 11

1 \ 2 \ 3 \ 4 \ 5 \ 6

首先拿到题目厘清题意，我们需要得到最后的结果，我们发现相当于是将 2--4 的连接插入到 1--5 的连接中，再将 3 插入到 2--4 的连接中。如果将 Tree 横过来，就更便于我们理解了。

正如上面我们所讨论的，这棵横过来的二叉树可以看做是由『一路向右』的 rightmost 的一个 path 将其他 path 串起来，这条 rightmost path 我们称为『主 Path』，通过 right 进行连接。其他的 path 通过 left 来系到『主 Path』上，那么这就是一个将 Multilevel Linked List 拉直的过程嘛。因此我们可以看到另一个题目，Flatten a Multilevel LinkedList，和这道题可以说就是换了一个马甲。可以看到对于多层链表，和我们刚刚分析的就是一模一样的思路，因此可以一起解决了。

OK，那么分析出来思路了，怎么做呢？

由于 Binary Tree 是一个二维结构，我们没法像 Linked List 一样 while (cur.next != null) 进行遍历，但是我们可以这样思考，对于一维，我们从头到尾成线。对于二维，我们连线成面。也就是说，像我们以前基础数学的坐标轴一样，只要我们找到了 x 轴和 y 轴，我们就可以 cover 整个平面。对于二叉树这里，我们的 x 轴和 y 轴就是 left 和 right，只不过其中 right 作为主轴，从每一个坐标（Node）我们延伸出来 left 轴形成一个网状平面。

因此我们的思路就是 maintain 一个『一路向右』的遍历，同时对每一个 node，如果有 left 存在，就进入到下一层，对下一层继续进行『一路向右』的遍历，直到找到下一层的最后一个 node，将该 node 连接到上一层的下一个 node 的前面，从而完成了将下一层拉平到上一层的过程。这样 iterative 逐层向下进行，直到将最下面一层拉平，我们就完成了任务。我们来看图理解一下：

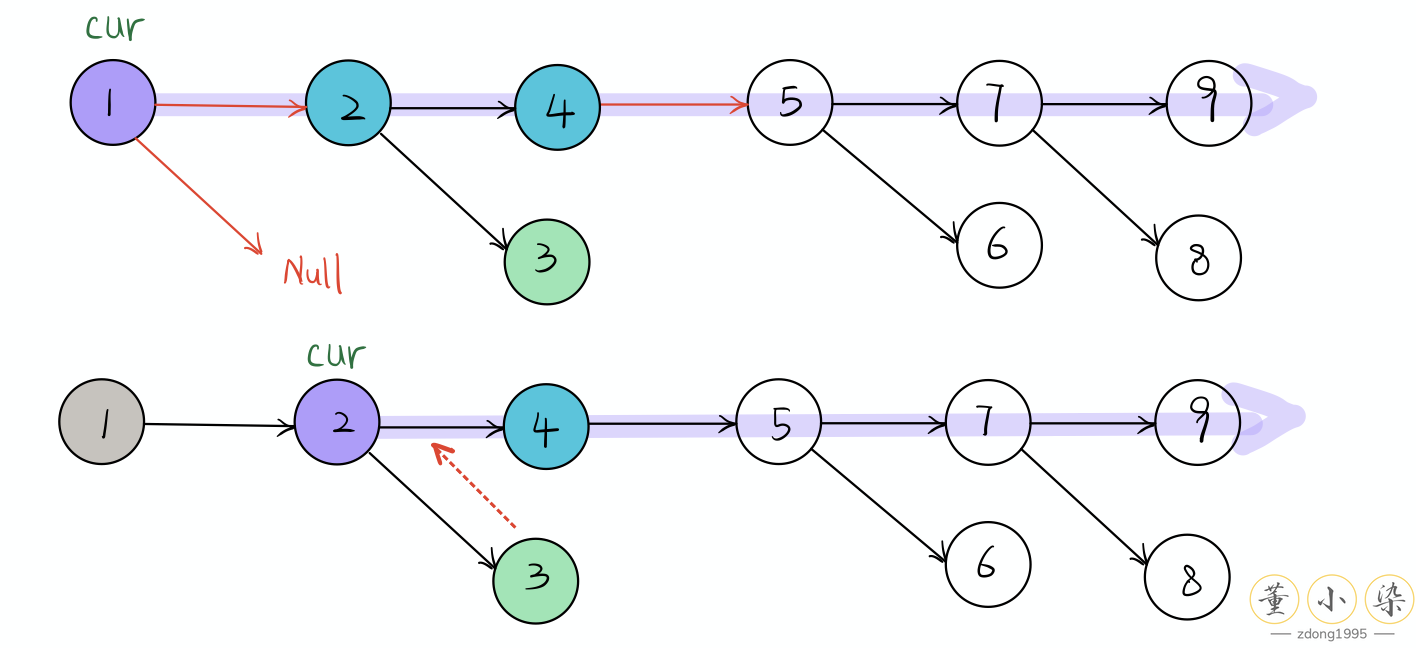
cur 从 root 遍历到 null 停止，如果 cur.left 存在，则沿着右子树 (next level 的 right path 看做 linked list) 遍历直到找到 tail node（4），将 tail 连接到 cur 和 cur.right 之间。

这样相当于将第二层的 linkedlist 向上连接到了第一层，向后遍历，继续同样的操作，直到将所有层的 LinkedList 都连接到了第一层，Done！

看懂了图，代码就非常简单了。就是 while 循环里再对每一层进行一个 while 循环即可，同样需要注意我们上一次 Linked List 技巧分享的 NPE Check 及 Delink 避免成环的技巧。如果你还没有看，快回去复习一下吧~另一道题 Mutltilevel Linked List 的代码基本一致，注意一下 prev 的 corner case 处理即可。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22

public void flatten(TreeNode root) {
    if (root == null) { // corner case
        return;
    }
    TreeNode cur = root;
    while (cur != null) { // traverse down along the rightmost path
        TreeNode next = cur.right; // store next node
        // flatten the left subtree to insert between cur and cur.right
        if (cur.left != null) {
            // find the tail of the right subtree of cur.left
            TreeNode tail = cur.left;
            while (tail.right != null) {
                tail = tail.right;
            }
            // connect the tail to stored next
            tail.right = next;
            cur.right = cur.left;
            cur.left = null; // delink
        }
        cur = cur.right;
    }
}

• Time Complexity: $O(N)$ ，每个 node 最多都遍历了两遍：
  • 在下一层的时候扫到 tail 的过程中遍历了一次
  • flatten 移到上层后向后扫的时候又遍历了一次
• Space Comlexity: $O(1)$，没有任何额外数据结构和 call stack 的使用

上面这个遍历思路有没有觉得很有意思呢，就是相当于一个 x 和 y 轴双向遍历二叉树这个平面网状结构而已。想想两层 for 循环遍历二维数组和两层 while 循环遍历二叉树，突然就开窍了呢。下面我们来看看另一种 iterative 的『真.逐层遍历』。

Tree 的 Iterative 『真.逐层遍历』

下面来看一道题目 LeetCode 116: Populate Right Node：

You are given a perfect binary tree where all leaves are on the same level, and every parent has two children. The binary tree has the following definition:

1 2 3 4 5 6

class Node { int val; Node left; Node right; Node next; }

Populate each next pointer to point to its next right node. If there is no next right node, the next pointer should be set to NULL.

Initially, all next pointers are set to NULL.

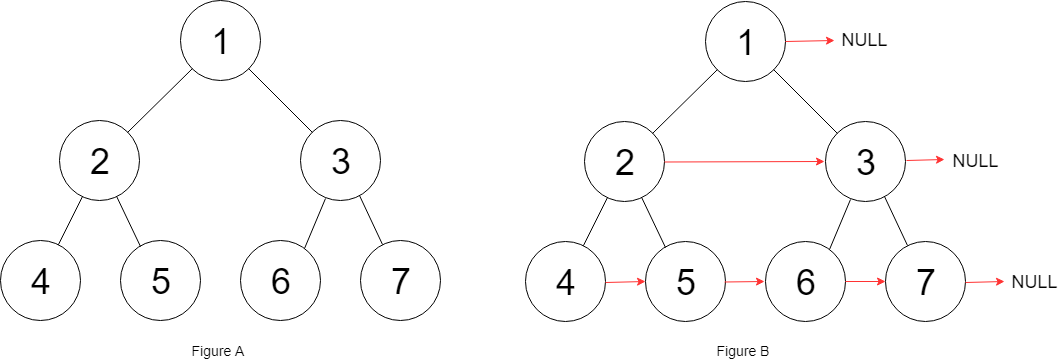
这个题目看得有点懵，我们来看一下图就懂了：

给定的二叉树是完美的，也就是每一层都是满的，除了 leaf node 每个 node 都有两个 child。现在我们的 TreeNode 不仅是存 left 和 right 了，还有一个 next 指向当前层的下一个 node，如果是最后一个 node ，直接指向 null 即可。大家看到这个题目，肯定第一反应是可以 BFS 进行 Level Order 遍历，对每一层一个一个进行连接 next 即可。如果我们不能使用额外空间呢，该如何操作？

之前我们讲过，BFS 就是一个批次的 iterative 操作，因此我们自然而然可以将 batch iteration 来细分拆成单独的 atomic iteration。首先来思考一下为什么我们 Level Order 遍历时需要使用一个 queue，我们需要一个队列来保持我们每一层『先进先出』的当前层里的左右顺序。我们每一层从左往右进行遍历，通过 queue 将相邻的 node 放在了一起，因此 queue 中的下一个元素就是我们同一 level 的相邻下一个 Node，这个时候只需要将 cur.next 连接到 queue 中的下一个 node 即可。

我们想不使用 queue 来 Iterative 解决的话，tricky 的部分在于如何 connect 两个不是同一个 root 的两个 node。如果每一个 node 可以存储一个 parent 指针的话，我们也可以通过

cur.right.next = cur.parent.right.left

从而将 right node 和下一个 left node 连接起来。可以看到只要能够解决 了cur.parent.right ，那我们就解决了这个问题。How?

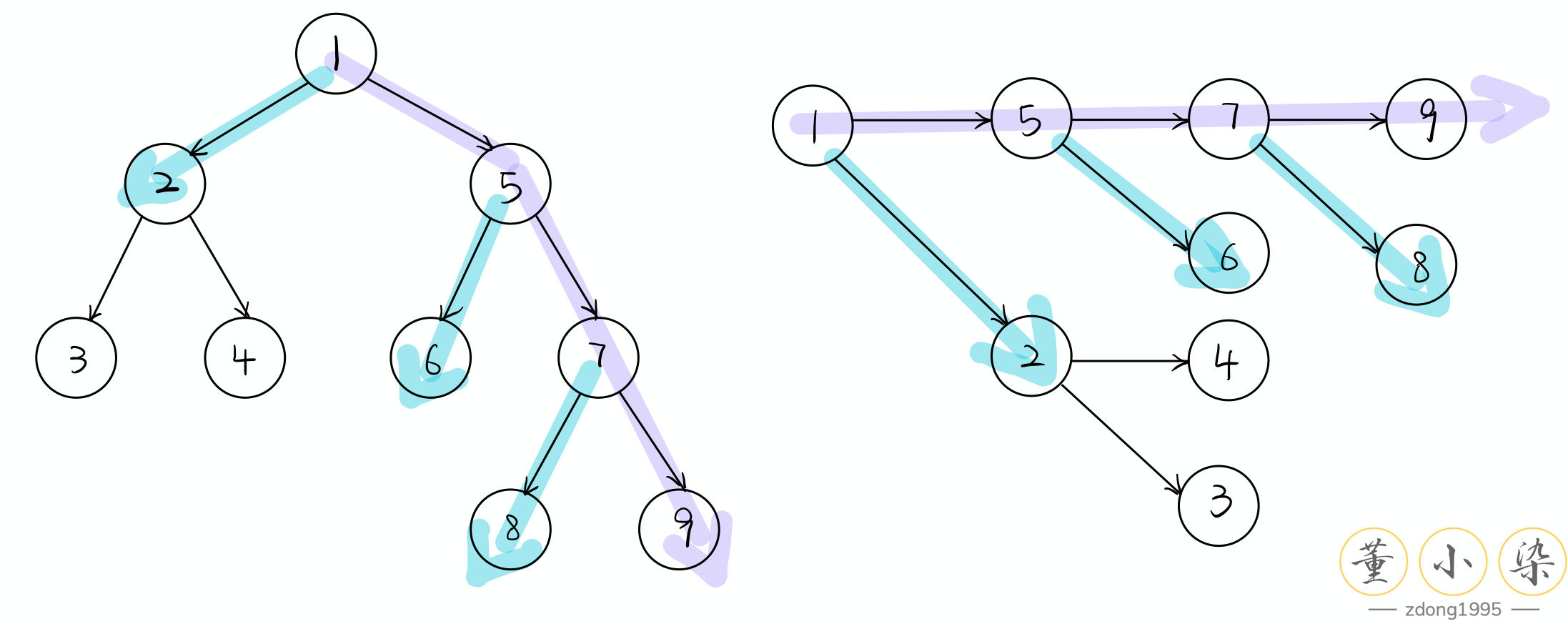
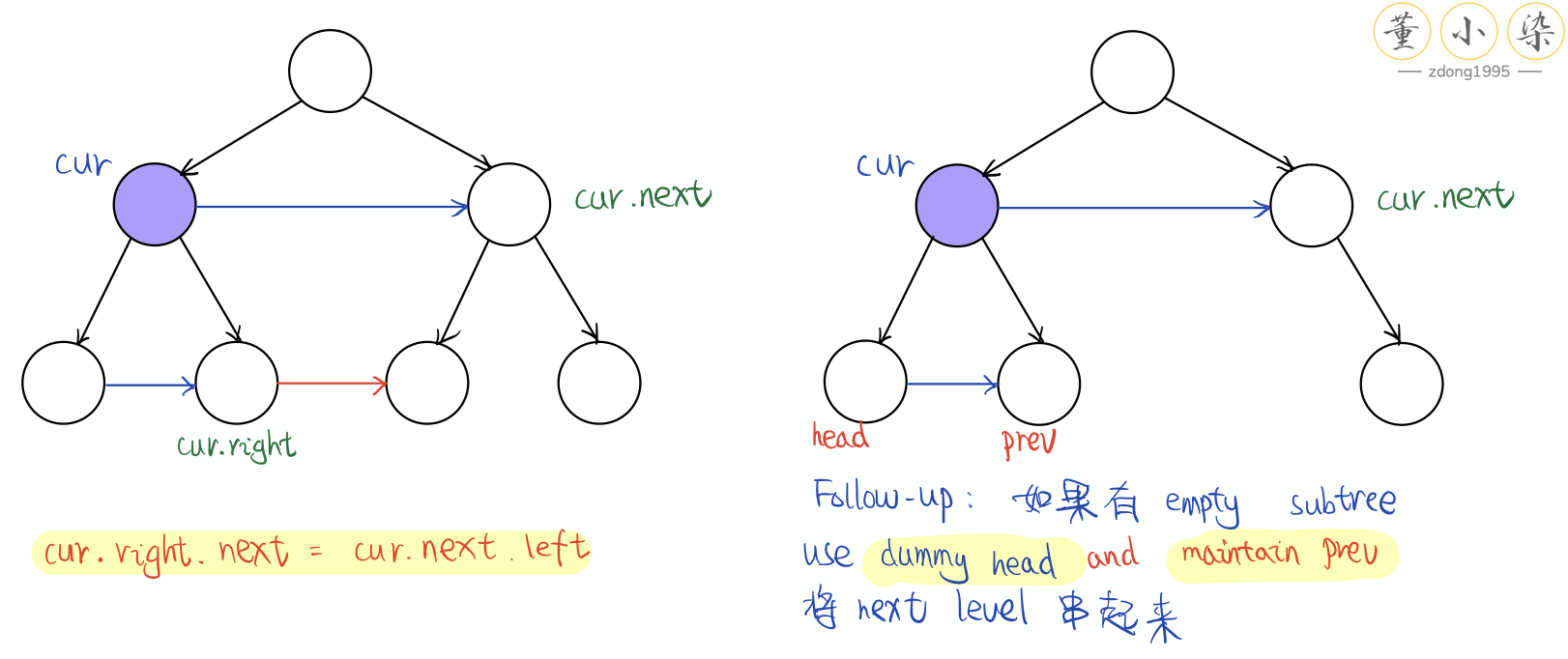
画个图，我们可以神奇的发现，cur.parent.right 就是 cur.next！

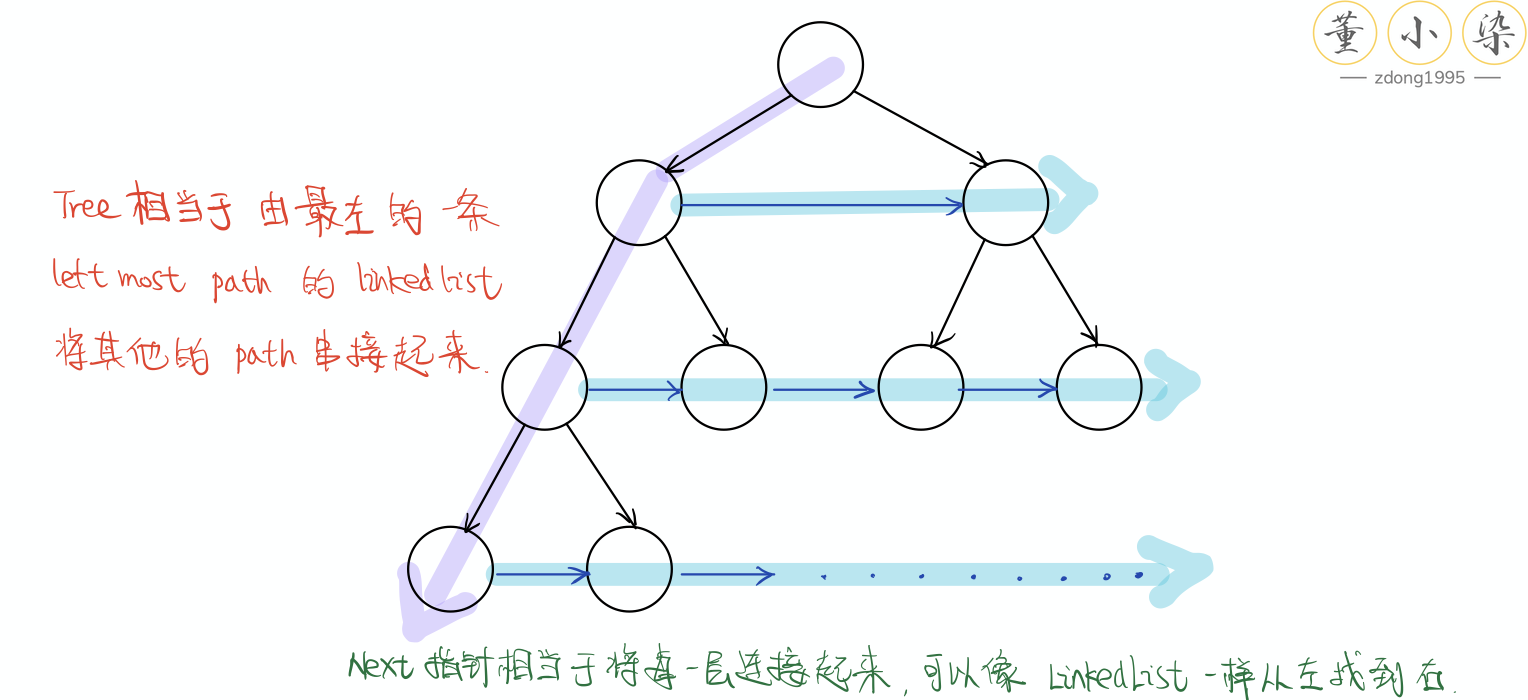
在这里我们由于需要从左往右遍历，因此可以将二叉树看做是由最左的一条 left most path 的 Linked List 将其他的 path 串接起来。这里的 next 指针相当于在每一层形成了一条 Linked List 将 TreeNode 从左至右连接起来。也因此此时的 Tree 可以自上向下看做一个 Multi-level LinkedList，是一个『真 Level Order』遍历。

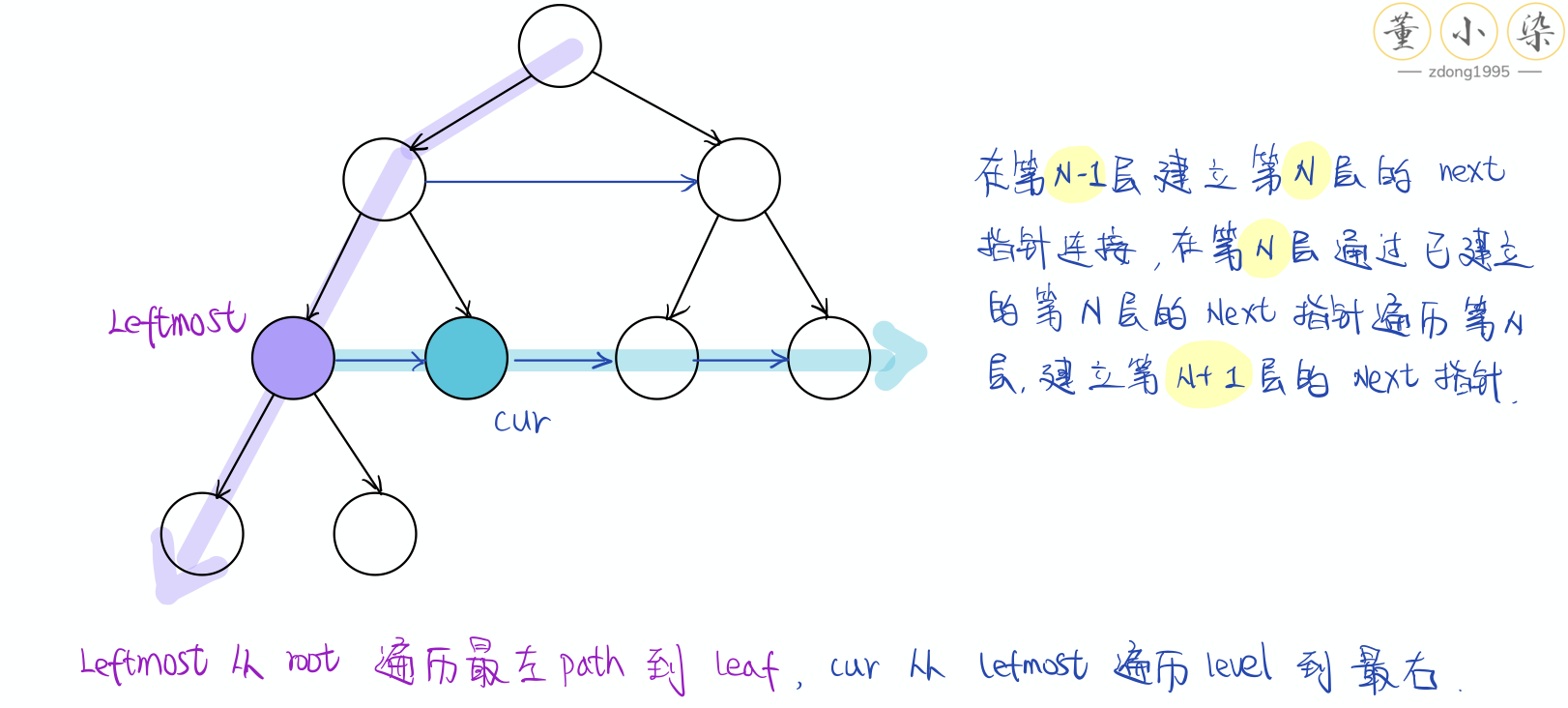
这道题目的关键是，为了保证在每一层我们可以遍历，我们需要有 next ，但是二叉树里的 ListNode 一开始又没有这个值，那么该怎么办呢？因此 key point 就是在上一层建立下一层的 next 连接！

在第 N-1 层建立第 N 层的 next 指针连接，在第 N 层时通过建立好的 next 指针连接来遍历整个 level，建立第 N+1 层的 next 指针，可以实现跨 root node 之间的 next 连接建立。因此有了上面的经验，我们可以轻松地写出两个方向的 iterative 遍历实现二维的遍历：

• leftMost 从 root 遍历到 left most path 的 leaf node

  Termination condition: while (leftMost.left != null)

• cur 从当前层 leftMost 遍历到最右

  Termination condition: while (cur != null)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22

public Node connect(Node root) {
    if (root == null) {
        return root;
    }
    Node leftMost = root;
    while (leftMost.left != null) {
        // start from the leftmost node, connect current level
        Node cur = leftMost;
        while (cur != null) { // traverse linked list of cur level
            // connect for same root nodes
            cur.left.next = cur.right;
            // connect for inter-root nodes
            if (cur.next != null) { // avoid NPE
                cur.right.next = cur.next.left;
            }
            cur = cur.next;
        }
        leftMost = leftMost.left;
        // traverse the left most path to arrive last level
    }
    return root;
}

这道题的 follow-up 是如果这个二叉树不是全满的该怎么办。我们可以利用上一次 Linked List 中提到的 dummy head 的思想，我们不需要每次去 maintain 一个 leftMost，因为可能是 null 找不到，我们可以使用 dummy node 来存储下一层作为一个 Linked List 的 head，从而简化我们的代码。

看懂了思路和图，代码就非常简单了：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

public Node connect2(Node root) {
   if (root == null) {
       return null;
   }
   Node leftMost = root;
   while (leftMost != null) {
       // start from leftMost node to traverse current level
       // and connect the next level
       Node cur = leftMost; // current node at current level
       Node dummy = new Node(0); // used to store head of next level
       Node prev = dummy; // the leading node of next level
       // use dummy to avoid null check to simplify implementation
       while (cur != null) {
           // traverse current level to connect next level node
           // populate prev.next to next node in the next level
           if (cur.left != null) {
               prev.next = cur.left;
               prev = prev.next;
           }
           if (cur.right != null) {
               prev.next = cur.right;
               prev = prev.next;
           }
           // move to next node in current level
           cur = cur.next;
       }
       // move leftMost to left most node (head) of next level
       leftMost = dummy.next;
   }
   return root;
}

• Time Complexity: $O(N)$ ，每个 node 最多都遍历了一次
• Space Comlexity: $O(1)$，没有任何额外数据结构和 call stack 的使用

Summary

今天分享了从一维到二维的 iterative 的过程和一些思考，希望对你有所启发和帮助。对于第一种『伪逐层遍历』，其实适用性会广泛很多，稍微修改一下就是有名的高阶二叉树遍历算法 —— Morris 遍历。Moorris 遍历可以实现 $O(1)$ 空间消耗的前序、中序、后序遍历。这里只是实现了一种遍历，大家有兴趣的话可以自己研究一下。

对于第二种『真.逐层遍历』，之所以可以实现是因为题目中有了 next 指针，同时也帮助我们将 BFS 进行层级遍历的过程一窥究竟。使用 queue 进行 batch iteration 的过程就是这样的小的 iterative 过程的聚合。

同时我们也可以看到，我们二叉树每个 node 是连接两个 node，因此可以自己手写嵌套 while 循环进行二维遍历。如果是 N 叉树，或者是图呢？这也就是为什么我们需要高阶搜索算法如宽度优先搜索 BFS，深度优先搜索 DFS 等的原因。毕竟，人脑能装几个叉啊，人脑能 call 几层 stack 啊，编程就让算法高效办事，我们负责岁月静好。大家晚安！

光看不练等于没见

趁热打铁，快去解决今天的题目吧：

• LC114: Flatten Binary Tree to Linked List
• LC430: Flatten a Multilevel Doubly Linked List
• LC116: Populating Next Right Pointers in Each Node
• LC117: Populating Next Right Pointers in Each Node II

最后，如果这篇文章讲解对你有所帮助，欢迎分享给需要的人。谢谢！

欢迎关注我的微信公众号『董小染』。